刷题顺序按照:https://leetcode.cn/studyplan/coding-interviews/
本题解中标题是链接,会直接跳转到leetcode界面,如果想要跳转到页面指定位置,需要点击目录前的小数字
剑指 Offer 05. 替换空格
关键点:替换字符串
方法一:正则表达式 \s匹配空格
时间复杂度O(nm), n代表输入字符串长度,m代表正则表达式长度
String的replaceAll(regex, input)方法,方法返回一个处理的结果,要记得接收处理结果
方法二:考虑String不可变特性,使用StringBuilder逐个添加字符
时间复杂度O(n), n为输入字符串长度
识别当前char是否是空格,是则追加%20到Stirngbuilder中,否则添加当前char到StringBuilder中
原思路:

不足之处:无法判断 “+++” “+” “–“之类的符号
改进:
- 使用了Character自带的isDigit()方法判断当前字符是否是一个int
- 符号位的判断由循环改成单次,避免了 +++ +-这种情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public int strToInt(String str) {
if (str == null || str.length() == 0){
return 0;
}
int i = 0;
int n = str.length();
long res = 0;
char[] charArray = str.toCharArray();
int sign = 1;
//去除空格
while (i < n && charArray[i] == ' '){
i++;
}
//首先需要判断下标是否会越过数组长度
//判断符号位是否存在,存在的话是什么,这里不用循环,就可以避免“+++”、“+-+”这种情况
if (i < n && (charArray[i] == '+' || charArray[i] == '-')) {
sign = (charArray[i] == '-') ? -1 : 1;
i++;
}
//判断数字位,并且在添加下一个数之前判断是否溢出
while (i < n && Character.isDigit(charArray[i])){
//res*10之后可能会越界导致数据溢出,造成结果不准确,所以一开始的res要用long类型
long tmp = res * 10 + charArray[i] - '0';
//判断是否会越界
//这里要带上符号位来比较大小
if (tmp * sign > Integer.MAX_VALUE){
return Integer.MAX_VALUE;
}else if (tmp * sign < Integer.MIN_VALUE){
return Integer.MIN_VALUE;
}
//这里先不急着赋予符号位,因为给了符号之后就不好使用res * 10 + charArray[i] - '0'来得到下一个数了。所以res在函数结尾return的时候才带上符号位
res = tmp;
i++;
}
//带上符号位
return (int)res*sign;
}
}
|
在解决这个问题时,我们可以考虑逐步分析题目要求,并制定相应的解决方案:
-
首先,我们需要丢弃开头的空格字符。这可以通过迭代字符串,跳过空格字符来实现。
-
接下来,我们需要处理符号位。如果第一个非空字符是正号或负号,我们需要记录符号位,并将指针向后移动一位。
-
然后,我们需要处理数字字符。从当前位置开始,我们可以通过迭代字符串,判断字符是否是数字字符,并将其转换为对应的整数值。
-
在处理数字字符的过程中,我们需要注意可能的溢出情况。因为题目要求假设环境只能存储32位大小的有符号整数,所以我们需要检查结果是否超出了这个范围。
-
最后,我们将符号位乘以结果的整数值,并返回最终结果。
这个解决方案的关键是理解题目的要求,并根据要求逐步实现对字符串的处理。需要注意的是,我们使用long类型来存储中间结果,以应对可能的溢出情况。并且,在最后返回结果时,需要进行强制类型转换为int类型。
通过仔细阅读题目要求,将其转化为具体的解决方案,并使用逐步迭代的方式进行实现,可以帮助我们设计出符合要求的解决方案。
剑指 Offer 35. 复杂链表的复制
原思路:
复制链表,所以每个节点都是新的
使用map记录每个节点和其相对位置,第一次遍历链表,把所有节点作为key全部放入map,value默认-1。
第二次遍历,对map中每个key指出对应的value作为顺序下标
不足之处:无法顺序遍历每个节点,即使遍历了,也难以复制出新的节点
解法:两次遍历,第一次map中存入旧节点作为key,新节点作为value;第二次将value中的节点建立联系,由于key和value的顺序在第一次遍历中已经确定,且key的相对顺序也被确定,所以可以方便的找到对应顺序的value
要想到使用哈希表来复制复杂链表,可以按照以下思路进行分析:
-
首先,我们要理解题目中对复杂链表的定义。复杂链表中的每个节点除了有一个next指针指向下一个节点,还有一个random指针指向链表中的任意节点或者null。
-
我们可以考虑使用哈希表来辅助复制链表。哈希表可以将原节点和对应的新节点进行映射,以便在建立新链表的时候能够快速找到对应的节点。
-
解决这个问题的关键是在复制过程中正确处理random指针的指向。由于random指针可能指向任意节点,我们需要保证在哈希表中能够找到对应的新节点。
-
我们可以通过两次遍历链表来完成复制过程。第一次遍历时,我们创建新节点,并将原节点和新节点的映射关系存储到哈希表中。第二次遍历时,我们根据原节点的next和random指针,设置新节点的next和random指针。
-
最后,返回新链表的头节点。
通过按照题目要求的规则进行分析,并结合哈希表来辅助复制过程,可以想到使用哈希表来复制复杂链表的解决方案。
在实际编码过程中,我们需要熟悉哈希表的使用,并合理设置节点映射关系。同时,需要注意处理边界情况,如空链表和random指针为null的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public Node copyRandomList(Node head) {
//这里判断条件不能有head.next==null,否则会导致下面对应的value节点不能正常生成
if (head == null) {
return head;
}
Map<Node, Node> nodeMap = new HashMap<>();
Node p = head;
//第一次遍历:复制节点值建立新节点,利用map映射使得新节点顺序和旧节点顺序一致,
while (p != null){
Node newNode = new Node(p.val);
nodeMap.put(p, newNode);
p = p.next;
}
p = head;
//第二次遍历: 建立新结点之间的关系,即:建立新节点的 next 和 random 指针
while (p != null){
//使用p作为旧链表的指针, 把p当成旧节点,这样我们就可以不通过map的key来知道旧节点的next和value了
Node newNode = nodeMap.get(p);
newNode.next = nodeMap.get(p.next);
newNode.random = nodeMap.get(p.random);
p = p.next;
}
return nodeMap.get(head); // 返回新链表的头节点
}
}
|
思路:head为null直接返回head。使用虚拟头节点dummy连接原来的链表,方便head.val为目标值的时候删除head。使用pre指针始终作为前一个节点来辅助,cur指针指向当前节点,不断地遍历节点,如果cur.val为目标值,那么借助pre删除cur,直接返回整条链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public ListNode deleteNode(ListNode head, int val) {
if (head == null) {
return head;
}
ListNode dummy = new ListNode(-1);
ListNode pre = dummy;
pre.next = head;
ListNode cur = dummy.next;
while (cur != null) {
if (cur.val == val) {
pre.next = cur.next;
return dummy.next;
}
cur = cur.next;
pre = pre.next;
}
return dummy.next;
}
|
直接上思路:两个指针p1、p2分别指向headA与headB,当p1走到null,让他从headB开始走,p2同理,然后第二次走就会相遇,相遇(两者相等)时直接返回。即使两个都走到null,那么也是相等的,也可以返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == headB) return headA;
if (headA == null || headB == null){
return null;
}
ListNode pA = headA;
ListNode pB = headB;
while (pA != pB) {
pB = pB.next;
pA = pA.next;
if (pA == pB) return pA;
if (pA == null) {
pA = headB;
}
if (pB == null) {
pB = headA;
}
}
return pA;
}
|
原思路:去除字符串前后空格 -> 创建list保存每一个单词(含标点符号), 创建StringBuilder方便逐个添加char成为单词,将s改成charArray便于遍历取值 -> 逐个遍历数组字符,如果遍历到了空格字符,则判断SB是否是空格或空串,如果不是空串或空格,那么就把SB存到list中,清空SB继续遍历。如果当前字符不是空格字符,那么直接加到SB当中 -> 遍历结束之后,考虑到最后一个单词的SB还没存进去,所以存进去之后清空SB -> 逆序遍历List,每次加上一个存入SB –》返回时删除最后的空格再返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public String reverseWords(String s) {
//删除前后的空格部分
s = s.trim();
List<String> list = new ArrayList<>();
StringBuilder stringBuilder = new StringBuilder();
char[] charArray = s.toCharArray();
//开始读取单词部分
for (int i = 0; i < charArray.length; i++) {
if (charArray[i] == ' ') {
//说明不存在空格或SB不是空字符串,是我们想要的要的SB
String curStr = stringBuilder.toString();
//改成 if (curStr != "") 也可以通过测试
if (curStr != " " && curStr != "") {
list.add(curStr);
stringBuilder.delete(0, stringBuilder.length());
}
}else {
stringBuilder.append(charArray[i]);
}
}
if (stringBuilder.indexOf(" ") == -1) {
list.add(stringBuilder.toString());
stringBuilder.delete(0, stringBuilder.length());
}
for (int i = list.size() - 1; i >= 0; i--) {
stringBuilder.append(list.get(i) + " ");
}
return stringBuilder.delete(stringBuilder.length() - 1, stringBuilder.length()).toString();
}
}
|
其实也不需要判断是否是空格字符串,只需要判断空串也能达到目的
代码更简洁的思路:双指针
使用一个StringBuilder B,用来存储最终结果。使用trim()删除函数接收到的字符串的前后空格得到新的s –》对s从后往前遍历,定义两个指针i j,遍历开始前都指向s的最后一个字符,让i往前走,遇到第一个空格停下,使用subString(i+1,j)截取到这个单词加上空格存到B中 –》i继续跳过空格且不超过s的头部字符,直到遇到字符停下来,让j跳到i+1的位置,继续遍历 –》 遍历结束后,再使用trim()删除前后的空格返回结果
双指针细节:
-
对s进行清空前后空白字符的操作
-
先让left指针移动到s中空白区,也就是 while(left>=0&&s.charAt(left)!=' ')
-
存储下此时left和right之间的字符串
-
接下来让left指针移动到s中非空白区,也就是while(left>=0&&s.charAt(left)==' ')
-
修改right指针的位置,让他到达left指针后面,也就是空白区的第一个位置
-
循环继续
上面中的第2步和第4步使得left指针能在s中的字符区和空白区进行移动,并且保证了先走出字符区,再走出空白区
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
public String reverseWords(String s) {
/*
"the sky is blue"
字符区[空白区]字符区[空白区]字符区[空白区]字符区
*/
int left = s.length() - 1;
int right = left + 1;
StringBuilder sb = new StringBuilder();
//trim保证了left指针一开始就是在字符区
s = s.trim();
while (left >= 0) {
//先让left指针移动到空白区,使得left和right能包裹住这片字符
//只要移动了left,一定要保证不会越界,当left走到第一个位置的时候,还会执行left--,这就会导致越界
while (left >= 0 && s.charAt(left) != ' '){
left--;
}
//情况一:此时left走到了空白区的最后一个位置, 我们把字符区给截取下来
//情况二:此时left为-1,越界,我们也可以截取下来
sb.append(s.substring(left+1, right));
sb.append(" ");
//接下来让left指针走出空白区
while (left >= 0 && s.charAt(left) == ' ') {
left--;
}
//现在left指针走到了字符区,修改right指针的位置,重复循环
right = left + 1;
}
return sb.toString().trim();
}
|
易错点:再push的时候条件要搞清楚,要满足两个条件,①min队列为空时可直接加入 ②min队列最小值大于等于当前push的数字时,可直接加入min
如果没考虑等于最小值也能入最小栈的情况,就可能把push部分写成:
1
2
3
4
5
6
|
if (min.size() != 0){
int tmp = min.peekLast();
min.addLast(tmp >= x ? x : tmp);
}else {
min.addLast(x);
}
|
下面是通过代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class MinStack {
Deque<Integer> deque;
Deque<Integer> min;
/** initialize your data structure here. */
public MinStack() {
deque = new ArrayDeque();
min = new ArrayDeque();
}
public void push(int x) {
deque.addLast(x);
if (min.size() == 0 || min.peekLast() >= x){
min.addLast(x);
}
}
public void pop() {
int x = deque.pollLast();
if (x == min.peekLast()) {
min.pollLast();
}
}
public int top() {
return deque.peekLast();
}
public int min() {
return min.peekLast();
}
}
|
错误的push思路:
1
2
3
4
5
6
7
8
|
//添加大于队列中的元素到max队列中,这里的逻辑有问题,如果总是添加了大的到最前面,那么无法判定是否第一个是最大的
//所以这里的思路是有问题的
public void push_back(int value) {
deque.addLast(value);
if (max.size() == 0 || max.peekLast() <= value) {
max.addFirst(value);
}
}
|
正确的思路:对于将要添加的元素x,从max的最后一个元素开始向前逐一比对判断,如果x大于当前元素,则直接删掉(因为此时x在主队列中肯定是最新的,根据队列先进先出的特性,所以旧的那些可以不要)。
等到把所有比x小的都删除,结束循环,将x添加到max中。
改进后的代码:
1
2
3
4
5
6
7
|
public void push_back(int value) {
deque.addLast(value);
while (!max.isEmpty() && max.peekLast() < value){
max.pollLast();
}
max.addLast(value);
}
|
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class MaxQueue {
Deque<Integer> deque;
Deque<Integer> max;
public MaxQueue() {
deque = new ArrayDeque<>();
max = new ArrayDeque<>();
}
public int max_value() {
return max.size() == 0 ? -1 : max.peekFirst();
}
public void push_back(int value) {
deque.addLast(value);
//要保留能和value相等的元素,所以判断条件里面不能写等于
while (!max.isEmpty() && max.peekLast() < value){
max.pollLast();
}
max.addLast(value);
}
public int pop_front() {
if (deque.size() == 0) return -1;
int res = deque.pollFirst();
if (res == max.peekFirst()) {
max.pollFirst();
}
return res;
}
}
|
关键点:
①Java二维数组的行数直接使用matirx.length得到
②使用上边界、下边界、左边界、右边界能很好的通过边界来帮助我们对这个矩阵进行遍历
③使用从0开始的下标index作为结果数组的下标,每遍历一个值都自增
思路:要按照顺时针顺序打印矩阵的元素,可以使用模拟的方法。
具体步骤如下:
-
初始化四个边界变量:left、right、top、bottom,分别表示当前矩阵的左边界、右边界、上边界和下边界。
-
初始化结果列表 result 用于存储按顺序打印的元素。
-
进行循环,直到左边界大于右边界或者上边界大于下边界为止:
-
从左到右打印当前上边界的元素,将它们添加到 result 列表中。打印完后,上边界 top 加1。
-
从上到下打印当前右边界的元素,将它们添加到 result 列表中。打印完后,右边界 right 减1。
-
如果上边界 top 小于等于下边界 bottom,保证下边界是没被遍历过的,然后从右到左打印当前下边界的元素,将它们添加到 result 列表中。打印完后,下边界 bottom 减1。
-
如果左边界 left 小于等于右边界 right,保证左边界是没被遍历过的,然后从下到上打印当前左边界的元素,将它们添加到 result 列表中。打印完后,左边界 left 加1。
-
返回结果列表 result。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public int[] spiralOrder(int[][] matrix) {
int rowCount = matrix.length;
if (matrix == null || rowCount == 0) return new int[]{};
int columnCount = matrix[0].length;
int left = 0, right = columnCount - 1, top = 0, buttom = rowCount - 1;
int[] res = new int[rowCount * columnCount];
int index = 0;
while (left <= right && top <= buttom){
//从左到右
for (int i = left; i <= right; i++) {
res[index++] = matrix[top][i];
}
top++;
//从上往下
for (int i = top; i <= buttom; i++) {
res[index++] = matrix[i][right];
}
right--;
//从右往左
if (top <= buttom){
for (int i = right; i >= left; i--) {
res[index++] = matrix[buttom][i];
}
buttom--;
}
//从下往上
if (left <= right){
for (int i = buttom; i >= top; i--) {
res[index++] = matrix[i][left];
}
left++;
}
}
return res;
}
}
|
建议多做一两遍~~
这题好有意思~~
看完题解后才有的思路
思路:
①建立一个辅助栈,然后遍历pop数组中每个元素。
② 为push列表建立一个下标index
③ a. 如果栈顶元素和当前遍历元素不相等,那么加入push数组中的元素到栈中,index自增,继续判断栈顶元素
b. 如果栈顶元素和当前遍历元素相等,那么弹出栈顶元素,继续遍历pop数组
④如果最终能将栈中的元素全部弹出,说明这个序列时正确的,此时stack为空
- 定义一个辅助栈,用于模拟压栈和弹出的过程。
- 遍历弹出序列,依次判断每个元素是否与辅助栈的栈顶元素相同。
- 如果相同,则说明当前元素是下一个要弹出的元素,可以将辅助栈的栈顶元素弹出。
- 如果不相同,则将压栈序列中还未入栈的元素依次入栈,直到找到与当前元素相同的元素为止。
- 如果最后辅助栈为空,说明弹出序列是压栈序列的一个合法弹出序列;否则,弹出序列不是压栈序列的一个合法弹出序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Deque<Integer> stack = new ArrayDeque<>();
int pushIndex = 0;
for (int curPop : popped) {
//条件应该是栈为空时必成成立,栈顶元素和当前遍历元素不相等时必成立
while (stack.isEmpty() || stack.peekLast() != curPop) {
if (pushIndex >= pushed.length) {
return false;
}
stack.addLast(pushed[pushIndex]);
pushIndex++;
}
//此时栈不为空且栈顶元素和当前遍历的值相等,那么弹出栈顶元素,让下标移动;
stack.pollLast();
//由于在循环中,进行了下标自增之后才判断栈顶元素是否和遍历元素是否相等,所以pushindex比栈顶元素在push数组中的位置更靠后,此处就不需要在自增了
//pushIndex++;
}
return stack.isEmpty();
}
}
|
类似二分的思想
思路:从矩阵的第一行最后一个元素开始查找 –》当前元素左边的都比他小,下面都比他大(二分的体现) –》 如果当前元素比target大,那么往下走,否则往左走 –》 循环终止条件时行指针不能大于等于行总数,列指针不能小于0 –》如果循环之后没找到,那么返回false
时间复杂度O(m+n), m为矩阵行数,n为列数,耗时最长情况是target在最后一行的第一个,此时需要完整的走完一列一行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
int rowCount = matrix.length;
if (matrix == null || rowCount == 0){
return false;
}
int columnCount = matrix[0].length;
int row = 0; // 指针row指向第一行
int column = columnCount - 1; // 指针col指向最后一列
while (row < rowCount && column >= 0){
if (matrix[row][column] == target) {
return true;
}else if (matrix[row][column] > target) {
//说明下面的行只会更大,那么我们后面只会在这一行不断地缩小column就能找到答案
column--;
}else {
//说明我们需要走到下一行更大的数字中去
row++;
}
}
return false;
}
}
|
2023/0706
稍微容易出错的地方:第二次遍历的应该还是字符串而不是int数组,因为只有原字符串的顺序才是合理的字符顺序,如果按照int数组的顺序遍历,遍历出来的是字母表中的第一个次数为一的字符而不是字符串中第一个次数为一的字符
思路:
使用int数组来记录次数,数组的下标为任一小写字符到字符a的距离,值为出现的次数 –》对字符串遍历,对当前字符对应的数组中的位置上的值自增 –》第一次遍历结束,字符串中所有的数字都有了出现的次数,对字符串进行第二次遍历,根据字符串中字符的顺序找到数组中次数为一的元素,此时字符串中的对应字符就是第一个次数为1的字符
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public char firstUniqChar(String s) {
if (s == null || s.length() == 0) {
return ' ';
}
int[] arr = new int[26];
Arrays.fill(arr, 0);
char[] chars = s.toCharArray();
for (char ch : chars) {
arr[ch - 'a']++;
}
for (char ch : chars) {
if (arr[ch - 'a'] == 1) {
return ch;
}
}
return ' ';
}
}
|
题目:请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
这题有一个很容易错的点:加入节点到队列的时候,是否需要根据当前层的层数判断加入节点的顺序?
不需要
只需要根据当前层数来控制加入的值应从队列前面加还是后面加。中间结果用队列来存,而不像其他的层序打印树的题一样用list存了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
Deque<TreeNode> nodes = new ArrayDeque<>();
Deque<Integer> resSubList = new ArrayDeque<>();
List<List<Integer>> res = new ArrayList<>();
nodes.add(root);
int level = 1;
while (!nodes.isEmpty()){
int size = nodes.size();
for (int i = 0; i < size; i++) {
TreeNode tempNode = nodes.pollFirst();
if (tempNode.left != null ) {
nodes.add(tempNode.left);
}
if (tempNode.right != null) {
nodes.add(tempNode.right);
}
//奇数层,按顺序加入
if (level % 2 == 1) {
resSubList.addLast(tempNode.val);
}else {
resSubList.addFirst(tempNode.val);
}
}
res.add(new ArrayList<>(resSubList));
resSubList.clear();
level++;
}
return res;
}
}
|
2023/0708
多写几次熟悉熟悉
1
2
3
|
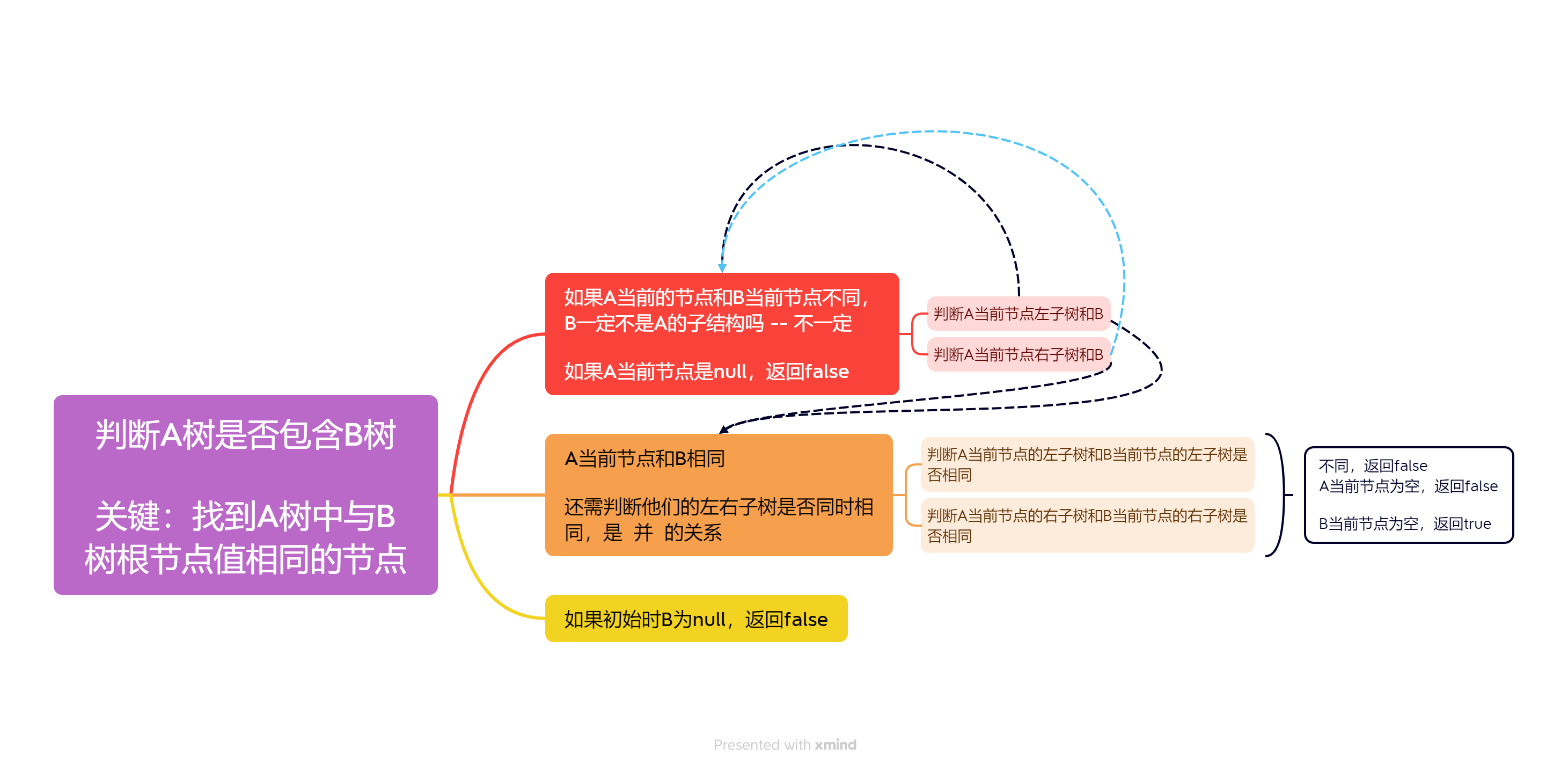
题目:输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
|
容易忽略的点:B可以是A的中间一部分结构,而不需要满足是到某个非叶子节点到叶子节点的结构
思路:目前仅有的函数是判断是否为子结构,但是这能让我们直接判断出来吗?显然是不行的,判断是否为子结构,就必须要去判断某个部分是否相等,所以我们应该单独写一个函数判断两棵树是否相等,我们将函数定义为boolean isSameTree(TreeNode A, TreeNode B)
对于isSameTree函数,我们想想什么时候函数应该返回true,什么时候返回false
如果我们要让函数返回false,那么就应该判断树的每一个节点是否都相等,如果不相等,那么就应该返回false。
那么不相等有什么情况呢:1. A的节点此时为null了,那么就不行了 2. A的val与B的val不相等。
上述两种情况就是false的情况。
那么什么时候返回true呢?我们现在要判断这两个树是否相等,显然当B为null的时候,说明B之前的节点都能顺利走完了,所以到B为null的时候整颗树B都已经校验完了,此时应该返回null。
当我们确定了返回true、false的条件之后,还需要考虑经过了判断条件之后怎么继续进行下一步,当前经过判断条件之后,我们把当前节点确认了,那么接下来就应该确认这两个节点的左右节点,所以我们给他们的左右节点做一个递归调用,将结果&&起来。这就完成了整个boolean isSameTree(TreeNode A, TreeNode B)函数的逻辑
接下来考虑如何在isSubStruct这个函数里面调用这个函数
对于isSubStruct,如果B为null,那么肯定返回false。
接下来就要考虑A的左子树和B是否能成为子结构 或者 A的左子树和B是否能成为子结构 或者 A本身是否和B同
这三个条件只要有一个满足,即可让整个函数返回true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
//自己调用自己时的终止条件或直接判断题目的输入参数是否满足要求
if (A == null || B == null){
return false;
}
return isSameStruct(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
private boolean isSameStruct(TreeNode A, TreeNode B) {
//自己调用自己时的终止条件
if (B == null) {
return true;
}
//自己调用自己时的终止条件
if(A == null || A.val != B.val) {
return false;
}
return isSameStruct(A.left, B.left) && isSameStruct(A.right, B.right);
}
}
|
思路:利用递归,终止条件为输入的节点为null,对于每一个节点,我们暂存其左子树,然后给左子树赋值整理好的镜像右子树,然后给该节点的右子树赋值整理好的镜像左子树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return root;
TreeNode tmp = root.left;
//把整理好的镜像右子树直接赋给左子树
root.left = mirrorTree(root.right);
//把整理好的暂存镜像左子树直接赋给右子树
root.right = mirrorTree(tmp);
return root;
}
}
|
思路:对于输入的节点,如果节点为null,则返回true,否则使用函数recur,当前节点的左子树和右子树作为参数,获取函数返回值进行返回 –》
在recur中,
如果接受的两个节点有一个为null,则返回false
如果接受的两个节点的值不同,则返回false
如果接收到的两个节点都为null,说明前面的层次都通过了,来到了叶子节点的子节点,此时返回true
递归调用recur,接收到的L、R节点,L的左子树和R的右子树作为参数、L的右子树和R的左子树作为参数。将调用结果 && 再作为返回值返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public boolean isSymmetric(TreeNode root) {
return root == null ? true : recur(root.left, root.right);
}
private boolean recur(TreeNode left, TreeNode right) {
if (left == null && right != null) return false;
if (left != null && right == null) return false;
if (left == null && right == null) return true;
if (left.val != right.val) return false;
return recur(left.left, right.right) && recur(left.right, right.left);
}
}
|
2023/0709
题目:

思路:这道题应该使用回溯算法,将矩阵中的每一个字符作为路径的开始,进行回溯。
确定递归的参数:
- 矩阵board:有了它才能知道当前的字符
- 行指针i
- 列指针j
- 目标字符串word
- 指向目标字符串当前的字符使用的索引wordIndex
- 当前位置是否已被其他路径访问的visited[][]数组
递归终止的条件:
- 返回true时的条件:当字符串的下标的大小等于字符串的长度,则返回true
- 返回false的条件:行指针越界、列指针越界、当前指向的字符不相等、当前位置已经被其他路径访问过
进入下一层前对于参数的处理:
- 将visited数组中对应位置标记为true
- 由于有四个方向,因此进入下一层要进入四次,每次只修改行或列
下一层处理完之后的结果:
- 如果下一层处理之后的结果为true,则直接返回true
- 否则,标记当前的visited位置为false,当前层返回false;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class Solution {
public boolean exist(char[][] board, String word) {
if (board == null || board.length == 0) return false;
int maxRow = board.length;
int maxColumn = board[0].length;
boolean[][] visited = new boolean[maxRow][maxColumn];
for (int i = 0; i < maxRow; i++) {
for (int j = 0; j < maxColumn; j++) {
if (dfs(board, i, j, 0, word, visited)) {
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, int i, int j, int wordIndex, String word, boolean[][] visited) {
//每次递归调用 dfs 时,index 参数表示当前正在匹配的 word 中的字符索引。
//如果能使得这一步的判断条件为true,那么表示前面的都已经匹配了,现在是最后一步
//当 index 的值等于 word.length() 时,说明已经匹配完整个 word 字符串,找到了符合条件的路径,可以返回 true。
if (wordIndex == word.length()) return true;
//这里是递归终止的第二种情况:失败
//如果当前的下标越界、当前字符不相等,那么就可以停止这一条路径的遍历
//如果当前位置已经被访问过,那么说明其他路径已经把这一个位置走了,我这条路径的下一步就不用走这个位置了
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != word.charAt(wordIndex) ||
visited[i][j]) {
return false;
}
//没越界、字符相等、这个位置没被其他路径访问过,那么我就得把这个路径给标记成已访问
visited[i][j] = true;
if (dfs(board, i+1, j, wordIndex+1, word, visited) ||
dfs(board, i, j+1, wordIndex+1, word, visited) ||
dfs(board, i-1, j, wordIndex+1, word, visited) ||
dfs(board, i, j-1, wordIndex+1, word, visited)) {
return true;
}
//我这条路径已经走完了,并且保证以指定初始起点开始遍历,没法得到正确结果,所以我应该把visited数组中对应的位置标记为false
//这样,当初始起点不同的时候,别的起点才能正常遍历他们自己的路径
//同时,也可以保证走到我这一步的起点的其他路径能正常访问
visited[i][j] = false;
return false;
}
}
|
这题debug了五六次才通过。
思路:这道题用的不是回溯,是搜索,所以不需要对visited数组做清除标记。用一个全局变量res记录能走的格子 –》
递归需要的参数:
- row:当前走到的行
- column:当前走到的列
- m:最大行数
- n:最大列数
- k:数位和最大值
- visited[][]: 格子是否被访问
递归终止条件:
进入下一层前需要做的处理:
- 将当前单元格标记为true
- res++ ,这里只需要一个res就能记录所有的答案,因为递归终止条件保证了我们不会走到其他路径走过的单元格,同时visited数组不会清除已经走过的标记,所以当前单元格标记为true之后,res++是合理的
进入下一层需要修改的参数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
int res = 0;
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
dfs(0, 0, m, n, k, visited);
return res;
}
private void dfs(int row, int column, int m, int n, int k, boolean[][] visited) {
//计算数位和
int count = 0;
int tempRow = row;
while (tempRow != 0){
count = count + tempRow % 10;
tempRow /= 10;
}
int tempColumn = column;
while (tempColumn != 0){
count = count + tempColumn % 10;
tempColumn /= 10;
}
//递归终止条件
if (row < 0 || row >= m || column < 0 || column >= n || count > k || visited[row][column]){
return;
}
//标记当前单元格已走过
visited[row][column] = true;
//能走的单元格数量+1
res++;
//走下一个格子
dfs(row+1, column, m, n, k, visited);
dfs(row - 1, column, m, n, k, visited);
dfs(row, column+1, m, n, k, visited);
dfs(row, column-1, m, n, k, visited);
}
}
|
tip:计算数位和可以单独抽取出来作为一个方法来进行调用,因为计算行、列的数位和过程是一样的,所以可以抽取
这里贴一个不使用全局变量,而是使用递归返回值作为答案的代码。
这个代码和我的代码的不同之处在于:
- 终止条件触发时,返回0,标志着现在这个单元格不能走,算成0个单元格
- 返回值是
当前单元格+后面能走的所有单元格之和 , 这一点很关键,是从当前单元格之后所有能走的单元格数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public class MovingCount {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
return dfs(0, 0, m, n, k, visited);
}
private int dfs(int i, int j, int m, int n, int k, boolean[][] visited) {
if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || getDigitSum(i) + getDigitSum(j) > k) {
return 0;
}
visited[i][j] = true;
return 1 + dfs(i - 1, j, m, n, k, visited)
+ dfs(i + 1, j, m, n, k, visited)
+ dfs(i, j - 1, m, n, k, visited)
+ dfs(i, j + 1, m, n, k, visited);
}
private int getDigitSum(int num) {
int sum = 0;
while (num > 0) {
sum += num % 10;
num /= 10;
}
return sum;
}
}
|
2023/0711
原失败思路:
递归终止条件:当前节点为null,同时如果当前累加值为target,则添加到res中
进入下一层前的处理:curVal加上当前节点的值,list存入当前节点
进入下一层的参数:最后的list结果、当前累加值curVal、目标值target、存储了路径上节点的list pathSum
回溯处理:从pathSum中删除当前节点
失败原因:一个叶子节点有两个null子节点,如果该条路径之和等于target,那么由于添加逻辑写在递归终止中,所以两个null节点会导致路径加了两次到res中
改进:
- 终止节点中不做添加正确路径到最后的list中
- 进入下一层前的处理改为:判断
当前节点是否是叶子节点(left和right同时为空)&& curVal加上当前值之后是否与target相同 ,如果为true,那么直接在叶子节点这一层加入路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int target) {
if (root == null) return new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
List<Integer> pathSum = new ArrayList<>();
reverseToSum(res, root, target, 0, pathSum);
return res;
}
private void reverseToSum(List<List<Integer>> res, TreeNode root, int target, int curVal, List<Integer> pathSum) {
if (root == null) {
return;
}
curVal += root.val;
pathSum.add(root.val);
if (curVal == target && root.left == null && root.right == null){
res.add(new ArrayList<>(pathSum));
}
reverseToSum(res, root.left, target, curVal, pathSum);
reverseToSum(res, root.right, target, curVal, pathSum);
pathSum.remove(pathSum.size() - 1);
}
}
|
2023/0712
这题最开始没看清楚是二叉搜索树,然后写了一个针对所有二叉树的算法,beats 2%左右😂
后来发现是二叉搜索树之后,根据面经和题目要求还想了很久
由于题目指定是二叉搜索树,所以按照中序遍历的顺序得到的节点顺序就是题目要求的链表元素的相对顺序
保持中序遍历的顺序很容易理解和实现,难点在于在当前节点怎么进行处理
思路:定义两个全局Node变量pre,head。pre负责始终指向前继节点、head负责指向链表开始节点
对于当前节点,我们要做三件事:
- 让当前节点的左指针指向pre
- 判断pre是否为null,如果为null,则说明当前节点是第一个节点,让head指向当前节点;如果不为null,那么让pre的右指针指向前继节点 —– 截止到第二部,已将完成了两个节点之间的互相指向
- 让pre移动到当前节点,pre=currentNode
结束遍历后,此时pre会指向链表中最后一个节点、head会指向第一个节点,我们还需要让他们相互指向,最后再返回head
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if (root == null) return root;
traverseInOrder(root);
//当我们完成中序遍历之后,pre会出现在链表的最后一个元素,head会指向第一个元素,我们现在要给
//这两个元素互相指向
head.left = pre;
pre.right = head;
return head;
}
private void traverseInOrder(Node root) {
if (root == null) return;
traverseInOrder(root.left);
//在当前节点应做的处理:
//我们先把cur拿出来, 不管当前pre是否有值,当前节点的左指针都应该指向pre
root.left = pre;
//如果pre不为null,那么让pre的右指针指向当前节点
if (pre != null) {
pre.right = root;
}else {
//否则,说明当前节点是第一个节点,应该让head也指向这个节点
head = root;
}
//pre此时完成了右指针的指向任务,应该移动到当前节点了
pre = root;
traverseInOrder(root.right);
}
}
|
二叉搜索树,按照正常中序遍历,肯定不知道啥时候出现第k大的节点,所以最容易想到的解法就是中序遍历这一个二叉搜索数,每次遍历的时候将遍历到的节点加入到list中。当我们遍历完之后,此时list中拥有所有的节点,要找到第K大的节点,则可以get(list.size()-k)
由于list在添加节点过程中会涉及到一个扩容的过程,所以它可能使得整个的效率非常的低下,那么这时候我们就需要想办法去改进的方法,就是我们将中序遍历给它反过来。正常中序遍历是先遍历左子树,然后遍历根节点,再遍历右子树,现在我们先遍历右子树,在遍历中间节点,最后遍历左子树。这样的话我们就得到一个从大到小的序列。
接下来还需要考虑:在这个遍历过程中,我们怎么样去判断当前这个节点的值是否是我们需要的呢?
那么这时候我们就需要一个全局变量z,在每一次对当前节点处理的时候,我们将这个全局变量Z-1, 如果减1之后它的值等于0,就说明此时就是我们需要找的第 K大的节点,然后这个时候我们要保存这个节点值,保存节点的方法就是维护第二个全局变量result,我们将这个第K大的节点的值赋值给result,后面即使你再遍历其他节点,也不会影响res的值,因为我K是一个全局变量,所以在其他节点处理的时候,将K减1之后发现K不可能再出现第二次等于0的情况,那么就保证了result只能被赋值一次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
int res, z;
public int kthLargest(TreeNode root, int k) {
z = k;
traverseInOrder(root);
return res;
}
private void traverseInOrder(TreeNode root) {
if (root == null) return;
//反着的中序遍历
traverseInOrder( root.right);
z--;
if (z == 0) res = root.val;
traverseInOrder( root.left);
}
}
|
注意,z一定要是全局变量,否则每个节点的z的值都不一样,就失去了z的作用😂
小小的优化:可以把递归终止条件改成if(root == null || z < 0) ,但是不改也能beats 100%了
解法一(比较容易想到):对根节点先序遍历子树得到深度,求差看看差是否小于等于1
容易出错的点:在返回最终结果的时候会忽略对根节点的左右节点的是否是平衡二叉树的判断
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
/*
* 要知道当前节点左右指数的深度之差是否大于一,那么就需要使用一个函数,它能够返回当前节点左右子树的深度
* */
int leftDepth = getDepth(root.left) ;
int rightDepth = getDepth(root.right) ;
//这里的返回值是最容易出错的,要记得判断左右子节点是否也是平衡二叉树。
return Math.abs(leftDepth - rightDepth) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
private int getDepth (TreeNode root) {
if (root == null) return 0;
int leftDepth = getDepth(root.left) ;
int rightDepth = getDepth(root.right) ;
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
}
|
由于每次都需要判断左右节点是否为二叉平衡树,因此时间复杂度就高了,$时间复杂度 = 每层执行复杂度 \times 层数复杂度 = O(N×logN)。$
最差情况下(为 “满二叉树” 时), isBalanced(root) 遍历树所有节点,判断每个节点的深度 depth(root) 需要遍历 各子树的所有节点 。
满二叉树高度的复杂度 O(logN) ,将满二叉树按层分为 log(N+1) 层;
解法二:保存子问题的结果,避免重复计算
关于这个优化到 O(n) 算法,我们可以从以下几个方面说明:
- 主要思路是在递归求解子问题时保存子问题的结果,避免重复计算。
- 在递归求树高函数 height() 中,我们不仅计算树高,还判断左右子树高度差是否 > 1。
- 如果左右子树高度差 > 1,直接返回 -1,表示这个子树不是平衡树,无需继续递归。
- 如果左右子树都平衡,则计算该节点的树高,并返回。
- 在函数 isBalanced() 中,如果 height() 返回 -1,则整棵树不平衡。如果返回 >= 0,则该树平衡。
- 这样就利用递归求解左右子树高度的同时,判断子树是否平衡,greatly减少了重复计算,降低时间复杂度。
- 每个节点只需要遍历一次,时间复杂度为 O(n)。
- 空间复杂度还是 O(n),为递归栈空间。
- 这种保存子问题结果,避免重复计算的思想,也是动态规划算法的核心。
所以这种优化主要利用的是递归遍历的特点,既能得到子树信息,又能做剪枝判断,从而提高效率。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public boolean isBalanced(TreeNode root) {
//如果树根节点高度是-1,说明树非平衡,返回false
return height(root) != -1;
}
public int height(TreeNode root) {
//递归终止条件
if (root == null) {
return 0;
}
//分别递归计算左右子树高度
int leftHeight = height(root.left);
//如果左子树已经非平衡,直接返回-1
if(leftHeight == -1) {
return -1;
}
int rightHeight = height(root.right);
//如果右子树已经非平衡,直接返回-1
if(rightHeight == -1) {
return -1;
}
//比较左右子树高度差
if (Math.abs(leftHeight - rightHeight) > 1) {
//如果左右子树高度差>1,返回-1表示非平衡
return -1;
}
//如果该节点平衡,则计算该节点树高
return Math.max(leftHeight, rightHeight) + 1;
}
}
|
题目:
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
思路:利用 && 的特性来实现递归的终止和继续
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public int sumNums(int n) {
return sum(n);
}
public int sum(int n) {
boolean x = n > 0 && (n = n + sum(n - 1)) > 0;
return n;
}
}
|
这个程序首先检查n是否大于0。如果是,它会计算n与sum(n-1)的和,并将结果赋值给n。这个递归调用将继续直到n为0,此时递归结束。最终的结果就是1+2+…+m。
注意,这个程序使用了逻辑与操作符(&&),这是一种短路操作符。如果其左侧的表达式结果为false,那么它就不会执行右侧的表达式。在这种情况下,当n等于0时,递归调用就会结束
20230716
二叉搜索树的特点:左子树<根节点<右子树
祖先:一个节点也可以是它自己的祖先
题目限制:p、q 为不同节点且均存在于给定的二叉搜索树中。
由题目限制可知,两个节点必定存在于树中,因此对树不停的遍历,一定可以找到节点
思路:对于根节点来说,p、q要么在左子树中、要么在右子树中、要么同时存在于左右子树中。p、q总有一个是大的,至于是哪个,暂且不管,我们假定p永远小于q,那么
- 当root比q大的时候,p、q都在root的左子树中,我们继续对root的左子节点进行同样的判断
- 当root比p小的时候,p、q都在root的右子树中,我们继续对root的右子节点进行同样的判断
- 当上面两条不成立的时候,则说明root的左子节点不会是q的祖先,root的右子节点不会是p的祖先,此时,root就是p、q的最近公共祖先
代码思路:交换p、q的指针,保证p的值是小的 –》 循环对root的值和p、q的值进行判断,满足思路第三点时退出循环,大于q时让root的左子节点成为新的root,小于p时让root的右子节点成为新的root。 –》 循环终止条件是root为null –》 函数返回root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val > q.val) {
TreeNode tmp = p;
p = q;
q = tmp;
}
while (root != null) {
if (root.val < p.val) {
root = root.right;
}else if (root.val > q.val) {
root = root.left;
}else {
break;
}
}
return root;
}
}
|
题目限制条件:p、q 为不同节点且均存在于给定的二叉树中。
思路:递归遍历根节点的右子树和左子树,如果在递归遍历的过程中能找到这个值相等的节点,则直接返回节点
递归参数:待判断的节点root、p、q
终止条件:这几个条件是或的关系
1. root==null,成立则说明现在到树之外了,直接把null返回给上一层,这样上一层就能知道他的右子树或左子树没有找到合适的节点了
2. root.val == p.val,成立则说明找到p了,直接把p返回给上一层
3. root.val == q.val,成立则说明找到q了,直接把q返回给上一层
下一层参数:root.left,p,q 和 root.right,p,q
结束递归之后的操作:
- 如果左子树没找到节点而右子树找到了,可知两个节点都在右子树中,并且最先找到的那个就是当前获取到的返回值,则直接return 对右子树递归遍历得到的节点
- 右子树没找到左子树找到了同理
- 左右子树都没找到节点,则说明我这个节点下面的左右子树是不包含目标节点的,
return null 告诉上一层我这个节点下面没有目标节点
递归函数返回值:root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null && right == null) {
return null;
}
if (left != null && right == null) {
return left;
}
if (left == null && right != null) {
return right;
}
return root;
}
}
|
2023/0717
2023/0718
剑指 Offer 16. 数值的整数次方
2023/0719
2023/0720
关键点:
1.复盘归并排序的整个过程
2.在拆分数组的时候要注意递归成立的条件是左指针小于右指针,不能等于,等于会造成mid=0时无限递归
3.统计次数在大于的时候统计,需将左边部分在当前数右边的数字也统计进去
4.在合并数组的时候,最后将数组复制回原数组的循环条件是left<=right , 因为只有left才能定位原数组的正确位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class Solution {
int count = 0;
public int reversePairs(int[] nums) {
if(nums == null || nums.length==0) return 0;
myMergeSort(nums, 0, nums.length-1, new int[nums.length]);
return count;
}
private void myMergeSort(int[] arr, int left, int right, int[] tmp) {
//这里不能写等于,因为mid向下取整,会导致left为0,right为1时mid为0,递归恒成立,栈溢出
if (left < right) {
int mid = left + ((right - left) >> 1);
myMergeSort(arr, left, mid, tmp);
myMergeSort(arr, mid + 1, right, tmp);
merge(arr, left, mid, right, tmp);
}
}
private void merge(int[] arr, int left, int mid, int right, int[] tmp) {
int le = left;
int ri = mid + 1;
int t = 0;
while (le <= mid && ri <= right) {
//注意这里要写等于,保证else中统计的是逆序对。如果不写等于的话else中会把等于的情况也统计进去
if (arr[le] <= arr[ri]) {
tmp[t++] = arr[le++];
}else {
tmp[t++] = arr[ri++];
//这里要考虑左边的都是有序的,所以是当前次数加一得到count+1,然后左边部分的在当前数字右边的数都要加一次所以mid-le
count = count + 1 + (mid - le);
}
}
while (le <= mid) {
tmp[t++] = arr[le++];
}
while (ri <= right) {
tmp[t++] = arr[ri++];
}
t = 0;
//注意这里是left<=right而不是t<=right,因为我们现在把数放回到原数组对应位置,只有left才能定位到原位置,t是不行的,
//t只能用来定位tmp数组
while (left <= right) {
arr[left++] = tmp[t++];
}
}
}
|
2023/0721
传递性及交换位置后必为最小值的证明看此题解
先给出快排代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
class Solution {
public String minNumber(int[] nums) {
myQuickSort(nums, 0, nums.length-1);
StringBuilder stringBuilder = new StringBuilder();
for (int i : nums) {
stringBuilder.append(i);
}
return stringBuilder.toString();
}
private void myQuickSort(int[] arr, int left, int right) {
int mid = left + ((right - left) >> 1);
//总是向下取整的中间值
int pivot = arr[mid];
int le = left;
int ri = right;
while (le < ri) {
while (arr[le] < pivot) {
le++;
}
while (arr[ri] > pivot) {
ri--;
}
if (le >= ri) break;
swap(arr, le, ri);
if (greaterThan(arr[ri], pivot) == 0) {
le++;
}
if (greaterThan(arr[le], pivot) == 0) {
ri--;
}
}
if (le == ri){
le++;
ri--;
}
if (left < ri) {
myQuickSort(arr, left, ri);
}
if (le < right) {
myQuickSort(arr, le, right);
}
}
private void swap(int[] arr, int le, int ri) {
int tmp = arr[le];
arr[le] = arr[ri];
arr[ri] = tmp;
}
}
|
对快排修改后的代码:
- 判断大小自定义了greaterThan方法,返回值为了避免等于号使用0、1、-1来保证指针能像原本快排那样正常移动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
class Solution {
public String minNumber(int[] nums) {
myQuickSort(nums, 0, nums.length-1);
StringBuilder stringBuilder = new StringBuilder();
for (int i : nums) {
stringBuilder.append(i);
}
return stringBuilder.toString();
}
private void myQuickSort(int[] arr, int left, int right) {
int mid = left + ((right - left) >> 1);
//总是向下取整的中间值
int pivot = arr[mid];
int le = left;
int ri = right;
while (le < ri) {
while (greaterThan(arr[le], pivot) == -1) {
le++;
}
while (greaterThan(arr[ri], pivot) == 1) {
ri--;
}
if (le >= ri) break;
swap(arr, le, ri);
if (greaterThan(arr[ri], pivot) == 0) {
le++;
}
if (greaterThan(arr[le], pivot) == 0) {
ri--;
}
}
if (le == ri){
le++;
ri--;
}
if (left < ri) {
myQuickSort(arr, left, ri);
}
if (le < right) {
myQuickSort(arr, le, right);
}
}
private void swap(int[] arr, int le, int ri) {
int tmp = arr[le];
arr[le] = arr[ri];
arr[ri] = tmp;
}
private int greaterThan(int a, int b) {
String bStr = String.valueOf(b);
String aStr = String.valueOf(a);
String aAddBStr = aStr + bStr;
String bAddAStr = bStr + aStr;
//拼接之后长度肯定一样,所以从最高位开始判断
for (int i = 0; i < aAddBStr.length(); i++) {
if (aAddBStr.charAt(i) > bAddAStr.charAt(i)) {
return 1;
}
if (aAddBStr.charAt(i) < bAddAStr.charAt(i)) {
return -1;
}
}
return 0;
}
}
|
2023/0722
关键点:如何确定数组中的数字是连续的?
答:要保证两个条件:1. 数组中最大值与最小值(不包括0,因为0会代表任意数)之差小于5 2. 数组中的数除了0能重复,别的都不能重复
同时满足上述两个条件则可确定数组中的数字是连续的
方法一:使用额外的变量min和max和Set在遍历数组时赋值,如果出现除0之外有别的重复数字,那么false,遍历结束之后有了min和max,就可以判断是否是连续的
方法二:对数组进行排序,排序结束之后对数组遍历,如果除0之外有别的数字和其下一个数字相等,那么返回false,最后用排序后的数组的最后一个元素和第一个元素之差判断是否连续
方法一代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> set = new HashSet<>();
//min初始超过牌堆数字的最大值,这样在遍历的时候才方便修改成最小值
int min = 15;
int max = -1;
for (int num : nums) {
if (num == 0) continue;
min = min < num ? min : num;
max = max > num ? max : num;
// 第一个判定条件:数组的值除了0之外不能重复
if (set.contains(num)) return false;
set.add(num);
}
//第二个判定条件:最小值与最大值之差应该小于5
return max - min < 5;
}
}
|
方法二代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public boolean isStraight(int[] nums) {
Arrays.sort(nums);
//定义joker的数量,让最小值指向的位置正确
int joker = 0;
for (int i = 0; i < 4; i++) {
if (nums[i] == 0) {
joker++;
continue;
}
if (nums[i] == nums[i+1]) return false;
}
return nums[4] - nums[joker] < 5;
}
}
|
堆插入的时间复杂度:O(logN)
从堆顶取元素的时间复杂度:O(1)
思路:空间换时间,利用堆的特性,将所有数放到两个堆中,小根堆A存储数值较大的那一部分的数,大根堆存储数值较小的那一部分的数。且我们始终保证奇数个元素的时候,小根堆的元素多于大根堆,那么中位数就在小根堆中
取值时如何取?
答:
- 当A、B中的元素个数相同的时候,取出两个堆的堆顶元素,求和然后除以2
- 当A、B中的元素个数不同的时候,中位数肯定是小根堆的堆顶元素
如何插入元素?—- 分情况讨论
情况一: 当堆A的元素个数和堆B的元素个数相同的时候,我们接下来使得小根堆的元素是较多的一方,那么能够直接把待插入的元素直接放到小根堆嘛?
肯定是不行的,待插入元素应该比大根堆的最大元素还要大才能插入小根堆中,现在因为我们不确定他和大根堆中的元素的大小关系,无法确定他会比大根堆中最大的元素大,所以不能直接插入小根堆,应该先把待插入元素插入大根堆,得到大根堆的最大值,然后把大根堆的最大值弹出放到小根堆,这样,小根堆的堆顶元素就是中位数了
情况二:当堆A的元素个数和堆B的元素个数不同的时候(小根堆会比大根堆多),我们应该使得两个堆的数量相同,那么我们能够直接将大插入元素插入大根堆吗?
当然也不行。待插入元素应该比小根堆的最小元素还要小才能直接将其插入大根堆,否则我们就应该从小根堆中挑选最小的数放入大根堆中,所以,应该先把待插入元素插入小根堆A,然后再从A中取栈顶元素放到大根堆B中。这样两个栈顶元素之和的一半就是中位数了
需要用到的Java知识:
PriorityQueue
需要得到大根堆时PriorityQueue的构造函数参数为PriorityQueue<>(Comparator.reverseOrder());
PriorityQueue底层比较时是c1.compareTo(c2),在使用了
PriorityQueue<>(Comparator.reverseOrder()); 之后,底层比较就会是c2.compareTo(c1);
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class MedianFinder {
Queue<Integer> A,B;
/** initialize your data structure here. */
public MedianFinder() {
A = new PriorityQueue<>();
B = new PriorityQueue<>(Comparator.reverseOrder());
}
public void addNum(int num) {
//接下来应该让A的数量更大
if (A.size() == B.size()) {
B.add(num);
A.add(B.poll());
}else {
A.add(num);
B.add(A.poll());
}
}
public double findMedian() {
return A.size() != B.size() ? A.peek() / 1.0 : (A.peek() + B.peek()) / 2.0;
}
}
|
2023/0724
思路:若要达到O(N)的时间复杂度,那么就是要只遍历数组,对于连续子数组和的最小值,我们可以这么考虑:
让数组的含义变成:到nums[i]前(包括nums[i])的连续子数组和的最大值,为了满足这个含义,我们需要遍历修改数组的值,修改方式如下:
使用一个额外的变量res记录数组的第一个元素的值,然后从第二个元素开始遍历数组nums,对于当前遍历到的元素,我们判断当前元素加上前一个元素(此时前一个元素的含义已经变成前面的最大连续子数组和了)之后的值和当前元素的值相比谁更大,将更大的值赋给当前元素nums[i],然后比较res和当前位置的值并更新res。
遍历结束后返回res
注意:res在此处是必要的,因为我们在修改数组的值的过程中,使用的是num[i-1]+nums[i], 数组的当前位置只能代表到他这里的最大和,但是如果他原本的值是负数,就会导致最大和变小,所以不能通过直接返回数组最后一位的方式来返回结果,只能用res去跟踪这个最大值。
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public int maxSubArray(int[] nums) {
if(nums.length == 1) return nums[0];
int res = nums[0];
for(int i = 1; i < nums.length; i++) {
nums[i] = Math.max(nums[i-1] + nums[i], nums[i]);
res = res > nums[i] ? res : nums[i];
}
return res;
}
}
|
跳了动态规划的题,直接到了位运算系列的题
思路:对于任一个二进制数,如果最后一位为1则这个数和1相与得1,如果最后一位为0则这个数和1相与得0;那么我们对二进制数n从最后一位开始&1,每&一次我们就对n无符号右移一位(无符号右移会补0),直到n变成0即可停止。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
//利用res记录每次&的结果,只有&得1时才会增加res
int res = 0;
//这里没法用fori循环,因为还不知道n的长度,而且用n的长度不如对是否为0进行判断,因为判断为0了就不需要考虑前面的位了,fori还需要把每位都走一遍
while(n != 0){
res += n&1;
n >>>= 1;
}
return res;
}
}
|
2023/0725
2023/0727
拿几个数试一试才能理解代码的逻辑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int add(int a, int b) {
while(b != 0) {
//得到进位,要想办法利用这个进位,怎么利用呢,那就是让b=c然后在下一次循环中求出a^b就能把进位算进去了。
//如果两个数相加之后没有进位,那么他们 & 之后的值位0,这样就能退出循环了
int c = (a & b) << 1;
//上一次循环得到的本位与当前的进位异或,这样就能得到各个位上的值
a = a ^ b;
//让进位进入下一次循环来求出 a^b的结果
b = c;
}
return a;
}
}
|
题目:一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
异或操作的特性:
- 与自身异或的结果为0:
a ^ a = 0
- 与0异或的结果是本身:
a ^ 0 = a
- 异或操作满足交换律:
a ^ b = b ^ a
- 异或操作满足结合律:
a ^ (b ^ c) = (a ^ b) ^ c
先说说如果只有一个数字是不同的情况下该如何找到这一个数:
根据异或的特点可以知道,两个相同的数异或得0,0和任意一个数异或会得到那个数本身,异或满足结合律,所以在一个数组中,由0开始异或,最后会得到那个唯一的数。
本题的难点在于现在又两个唯一的数,只用0异或得到的最后的数没法还原出两个数,所以需要将数组里面的数分组,两个唯一的数各一组,然后相同的数在同一组,那么该如何分组呢?
我们知道,对于数组里面所有的数从0开始异或之后,最后得到的数一定是两个唯一数异或的结果,那么对于两个不相等的数来说,他们的二进制位至少有一位是不同的,所以我们可以找出这个不同的位(该位经过异或运算肯定为1),又因为可能存在很多位不同,所以我们选择最低的一位,我们用1来开始逐位(使用 «1 就可以逐位了)找到这一位,把这个变量记作mask,初始值为1,如果mask & 异或结果不为0,说明mask找到了不同点,否则让mask二进制中的1继续前进。
现在我们有了mask,使用mask对数组里面的数分成两组,两个唯一数一定会被分成两个组,其他的数被分到哪组无所谓,因为同一对数字一定在同一组,分组的方式如下:对于唯一数A,A&mask为0时,唯一数B&mask一定为1,比如mask=0001 0000, A=1110 1111, B=0111 111,A和B在倒数第5位不同,所以会被分成两组。
我们使用变量a,b,赋初始值为0,分组的同时进行异或运算,这样数组遍历结束之后就得到了结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public int[] singleNumbers(int[] nums) {
//找到异或结果
int c = 0;
for (int num : nums) {
c ^= num;
}
//找到分组依据
int mask = 1;
while ((mask & c) == 0) {
mask <<= 1;
}
//利用a,b得到两组异或的结果
int a = 0, b = 0;
for (int num : nums) {
if ((num & mask) != 0) {
a ^= num;
}else {
b ^= num;
}
}
return new int[]{a, b};
}
}
|
题目:在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
判断某一位是否为1的方法:将那一位右移到最后一位,然后&1,其结果为1则知道那一位为1否则为0。
|表示按位或,在按位或运算中,任何一个操作数的对应位是1,结果位就是1。按位或通常用来设置位,比如 x = x | (1 << i) i要设置的位的下标
思路:使用一个32长度的数组bitCount,遍历输入的数组记录每一个数在32位上出现的次数,将数组遍历完之后,bitCount每一位就是所有的数字的对应位数之和,题目说除了唯一数之外的其他数都出现了三次,那么我们将bitCount中的每一位替换成对3取余之后的值,这个值就是唯一数在各个位上能出现的值。
同时,为了在替换过程中得到结果,我们使用|按位或运算来设置res的每一位,这样一次遍历bitCount就能得到最后的结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution{
public int getRes(int[] nums) {
//新建32长度的数组bitCount
int[] bitCount = new int[32];
for(int num : nums) {
for(int i = 0; i < bitCount.length; i++) {
//利用i得到对应位的值,这里实际上是逆序的,不是实际的数据,这是因为利用i更容易求得位数,读者也可以自行修改此处逻辑,我在这里逆序之后,下面还原的时候会把顺序也还原
bitCount[i] += (num >> i) & 1;
}
}
int res = 0;
for(int i = 0; i < bitCount.length; i++) {
//在将每一个元素取余3的同时求出结果, 要用 | 来设置位,同时因为i刚好和上面的顺序相反,所以顺序也能还原
res |= (bitCount[i] % 3) << i;
}
}
}
|
时间复杂度O(N)
空间复杂度O(1), 因为bitCount长度固定
2023/0728
本题有三种方法:hashMap求解、排序取中位数求解、摩尔投票法求解
| 方法名 |
时间复杂度 |
空间复杂度 |
| hashMap求解 |
O(N) |
O(N) |
| 排序取中位数 |
O(NlogN) |
O(1) |
| 摩尔投票法 |
O(N) |
O(1) |
综合来看,摩尔投票法的时空复杂度最优
摩尔投票法思路:对于一个数字,我们记录他的初始票数为1,让这个数字和其他数字接触,如果两数不相等,那么票数就减少1,相等则加一,当票数为0的时候,我们开始记录下一个数,循环上面的过程,直到数组遍历完。由于题目要求的数的票数超过数组长度的一半,所以这个数的票数肯定能保持到最后,其他数字的票数都会被消耗掉
一个形象的比喻:
玩一个诸侯争霸的游戏,假设你方人口超过总人口一半以上,并且能保证每个人口出去干仗都能一对一同归于尽。最后还有人活下来的国家就是胜利。那就大混战呗,最差所有人都联合起来对付你(对应你每次选择作为计数器的数都是众数),或者其他国家也会相互攻击(会选择其他数作为计数器的数),但是只要你们不要内斗,最后肯定你赢。最后能剩下的必定是自己人。
作者:知乎用户 链接:https://www.zhihu.com/question/49973163/answer/617122734
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public int majorityElement(int[] nums) {
//该变量记录当前得票最多的数字
int mostVotesNum = 0;
//该变量记录当前数字的票数
int votes = 0;
for (int num : nums) {
//如果票数为0,说明当前得票最多的数字应该换了
if (votes == 0) {
mostVotesNum = num;
}
//对votes的值进行修改
votes += mostVotesNum == num ? 1 : -1;
}
return mostVotesNum;
}
}
|
hashmap求解思路:利用map和两个变量res、times,res记录结果,times根据当前遍历到的数字进行更新,若当前遍历到的数字出现次数大于times,那么更新times和res,最后返回res;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int majorityElement(int[] nums) {
//该变量记录当前得票最多的数字
int mostVotesNum = 0;
//该变量记录当前数字的票数
int votes = 0;
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
if (map.containsKey(num)) {
map.put(num, map.get(num)+1);
}else {
map.put(num, 1);
}
if (votes < map.get(num)) {
mostVotesNum = num;
votes = map.get(num);
}
}
return mostVotesNum;
}
}
|
对于a[i]来说要求其除了他之外的所有和,最容易想到的就是将所有和的元素相乘,然后遍历的时候直接除去a[i]本身,但是由于题目限制不允许使用除法,所以这个方法不行
思路:对于a[i]来说要求其除了他之外的所有和,实际上就是求其左边所有数字的乘积 * 右边所有数字的乘积,所以我们可以创建两个辅助数组left和right,第一次遍历(顺序遍历)使得left[i]为a[i]左边所有的数字乘积,由于a[0]左边没有数字,所以left[0]=1.
第二次遍历(逆序遍历)使得right[i]为a[i]右边所有的数字乘积,由于a[a.length-1]右边没有数字,所以righ[a.length-1]=1.
第三次遍历我们可以直接修改a中各个位置的值,让a[i]=left[i]*right[i],这样我们就能得到答案了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public int[] constructArr(int[] a) {
if (a == null || a.length == 0) return a;
//left[i]表示a[i]的左边所有元素的乘积
int[] left = new int[a.length];
left[0] = 1;
//right[i]表示a[i]的右边所有元素的乘积
int[] right = new int[a.length];
right[right.length - 1] = 1;
for (int i = 1; i < a.length; i++) {
left[i] = a[i-1] * left[i-1];
}
for (int length = a.length - 2; length >= 0; length--) {
right[length] = a[length+1] * right[length+1];
}
//这里其实直接改a数组不用res数组也行,最后返回a即可
int[] res = new int[a.length];
for (int i = 0; i < a.length; i++) {
res[i] = left[i]*right[i];
}
return res;
}
}
|
数学知识:
均值不等式 $\sqrt{ab}≤(a+b)/2$
均值不等式推广式 :(n个正数相加)/n ≥ n次根号下(n个正数相乘)
$\frac{n_1+n_2+n_3+…+n_a}{a} \geq \sqrt{n_1n_2n_3*…*n_a}$
要求多个n相乘的最大值,那么就是找出一个长度x,使得a个x相乘的结果最大,又因为总长度为n, 则有函数 $y=x^a ==> y=x^\frac{n}{x}$ , 当n一定时,我们对 $y=x^\frac{1}{x}$求最值,发现最值点不是整数,接下来根据单调性找到离最值点最近的两个整数2和3,发现函数在带入3时是最大的,所以 函数$y=x^\frac{1}{x}$的最大值就是$f(3)$ , 也就是说,当长度x为3时,将长度n分成a段得到的函数最最大
函数单调性如下

由图可知,当x=3时取值最大。
思路:根据不等式、函数最值点、单调性可知,当x=3时,对n取a段长度为三的线段能让线段之积最大,但是如果n不是3的整数倍,就会出现余数1、2
对于余数为1的时候,我们需要知道f(n-1)*1和f(n-3)*4谁更大,这里的f(n-3)*4表示将一个3拿出来和1组合成2*2,经过计算后者一定大于前者,所以当余数为1的时候,我们要返回 3^(a-1)*4作为最终结果
对于余数为2的时候,说明最后一段的长度为1,由于Java中除法是向下取整的,所以还需要把最后一段乘进去
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n-1;
int a = n/3;
int b = n % 3;
if (b == 0) return (int) Math.pow(3, a);
//特殊点:当余数(即剩余的线段长度)为1时,需要将一个3拿出来,和1组合到一起成为2*2=4,来求得最大值
if (b == 1) return (int) (Math.pow(3, a-1)*4);
return (int) (Math.pow(3, a) * b);
}
}
|
2023/0729
思路和上一题是一样的,但是多了边界条件,所以需要考虑int32溢出的情况
第一版出错代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n-1;
int a = n / 3;
int b = n % 3;
if (b == 0) return pow(3, a);
if (b == 1) return pow(3, a-1) * 4 % 1000000007;
return pow(3, a) * b % 1000000007;
}
//快速幂
private int pow(int baseNum, int power) {
int res = 1;
while (power > 0) {
//奇数
if ((power & 1) == 1) {
res = baseNum * res % 1000000007;
power -= 1;
}
baseNum = baseNum * baseNum % 1000000007;
power >>= 1;
}
return res;
}
}
|
出错原因在于没有考虑到在快速幂中对于底数和结果计算的int类型越界问题。res = baseNum * res % 1000000007;有可能在右边计算乘法的时候已经越界了,那么越界之后对于1e7取模肯定也是错的。baseNum = baseNum * baseNum % 1000000007;这一行也是同理
改进代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n-1;
int a = n / 3;
int b = n % 3;
if (b == 0) return (int) pow(3, a);
if (b == 1) return
(int) (pow(3, a-1) * 4 % 1000000007);
return (int) (pow(3, a) * b % 1000000007);
}
//快速幂
private long pow(int baseNum, int power) {
long res = 1;
while (power > 0) {
//奇数
if ((power & 1) == 1) {
res = baseNum * res % 1000000007;
power -= 1;
}
//在这里转为long进行计算后再变成int,保证结果是正确的
baseNum = (int) ((long)baseNum * baseNum % 1000000007);
power >>= 1;
}
return res;
}
}
|
进一步修改,提高代码可读性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n-1;
int a = n / 3;
int b = n % 3;
long res = 1;
//使用switch来代替if,感觉更好些
switch (b) {
case 0: {
res = pow(3, a);
break;
}
case 1: {
res = pow(3, a-1) * 4 % 1000000007;
break;
}
case 2: {
res = pow(3, a) * b % 1000000007;
}
}
return (int) res;
}
//baseNum直接一开始就使用long类型接收参数
private long pow(long baseNum, int power) {
long res = 1;
while (power > 0) {
//奇数
if ((power & 1) == 1) {
res = baseNum * res % 1000000007;
power -= 1;
}
baseNum = baseNum * baseNum % 1000000007;
power >>= 1;
}
return res;
}
}
|
这题本来应该使用数学方法来求解,但是我选择了滑动窗口,如果之后有时间会将数学方法补上
滑动窗口解法:其实就是窗口内的总和大于target则左边界右移同时让总和减去旧的左边界,小于target则让右边界右移同时让总和加上新的右边界,等于则根据左边界值和右边界值生成一个数组存到list,然后让右边界右移同时总和加上新的右边界
易错点:1. 边界移动时忘记更新总和 2.相等时在得到答案序列后忘记让右边界右移和更新总和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> resList = new ArrayList<>();
int front = 1;
int rear = 2;
int sum = 3;
//初始时rear的值就比front大1,且front的值小于rear才会进入,这两个条件按证了至少有两个数字组成一个序列
while (front < rear) {
if (sum < target) {
rear++;
sum = sum + rear;
}else if (sum > target) {
sum -= front;
front++;
}else {
resList.add(getSubRes(front, rear));
rear++;
sum += rear;
}
}
return resList.toArray(new int[0][]);
}
private int[] getSubRes(int front, int rear) {
int[] arr = new int[rear - front + 1];
for (int i = 0; i < arr.length; i++) {
arr[i] = front++;
}
return arr;
}
}
|
一句话概括:数组延长后取模求实际位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public int lastRemaining(int n, int m) {
//因为我们知道最后删除的数字下标和数字的值是一样的,因为数组的元素从0开始,数组的下标也是从0开始
//由于最后留下的元素的数组下标一定是0.所以我们可以反推删除前的这个元素的下标,怎么推呢?
//我们可以很容易想到,最后一次剩下的数组长度为1,那么上一次的数组长度就是2
//我们可以假设上一轮的数量为当前剩余轮剩余个数+m,也就是让上一轮的数组长度的是(当前留下来的下标+待移动的步数)
//然后,由于实际数组的长度并没有这么长,所以我们要求出当前下标+待移动步数之后放到循环数组里面的真实下标,也就是对实际数组长度取模,循环上面的过程直到数组的长度到了最开始的长度n
//最后一次的下标是0
int ans = 0;
//从2开始,表义清晰一些,表示接下来要还原倒数第二轮的实际下标
for(int i = 2; i <= n; i++){
ans = (ans + m) % i;
}
return ans;
}
}
|
2023/0730
推荐题解:https://leetcode.cn/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/python3si-lu-dai-ma-10fen-zhong-jiang-qi-9btr/,视频+代码讲的都很好
这题是通过找规律来进行求解的。
思路:
将数字分区间,按一位数字、两位数字、三位数字分区间,一位数字的起始元素是1,这是为了保证规律能通用。
对于这些区间,我们加上几个关键概念给他们
- 数位位数:count,这个区间的数字需要使用多少位来表示,比如[1-9]区间每一个数字只占用一位,且有九个数字,那么这个区间的count就是9;区间[10-99]区间每个数字占用两位,且有90个数字,那么这个区间的数位位数就是180
- 区间首元素:start,表示这个区间开始的第一个数字
- 位数:digits,表示这个区间的数字是1位数还是2位数还是3位数
确定了上面几个概念之后,我们接下来进行三步操作
- 确定n所指向的数位在哪个区间中,这就需要n和count之间的大小关系来判断
- 确定具体的数num,这就需要使用start和n与dights之间的关系
- 确定数num中的第几位是我们需要的数字,这也需要使用start和n与dights之间的关系
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
class Solution {
public int findNthDigit(int n) {
if (n <= 9) return n;
//区间范围:[1-9] [10-99] [100-999]
//数字数量:9 90 900
//数位数量:9 180 2700
//位数: 1 2 3
//起始数字:1 10 100
//对初始区间第一位start进行初始化
long start = 1;
//对位数进行初始化,第一段区间的数字只有1位
int digits = 1;
//对区间内的数位数量进行初始化,第一段区间只有9个数字,这九个数字都是1位数,所以占用的数位数量是9
long count = 9;
//判断n剩余的位数是否还能大于指定区间的数位数量
while (n > count) {
//n要逐渐减去区间的数位数量,当n<=count说明n所在的区间找到了, 可以方便的表示出此时n在区间中的相对位置(此处相对位置可以理解成下标)
n -= count;
//让start、digits、count都变成下一个区间的对应值,start、digits是横向规律,count是纵向规律(也就是在同一区间找出等式)
start *= 10;
digits++;
count = 9 * digits * start;
}
//找到区间内的具体数字,也是找规律,可以用区间[10-99]尝试 start+n、start+n-1、start+(n-1)/2 发现只有最后一个能找到正确的数字
//这里使用额外的变量num来记录找到的数字,当然也可以修改start来记录因为后面也不需要区间初始值这个含义了
long num = start + (n-1) / digits;
//找到这个数字中那一位是我们需要的
int homologousDigit = (n-1) % 10;
//获取对应的数字
return Long.toString(num).charAt((n - 1) % digits) - '0'; // 3.
}
}
|
参考文档
Markdown语言——数学公式




