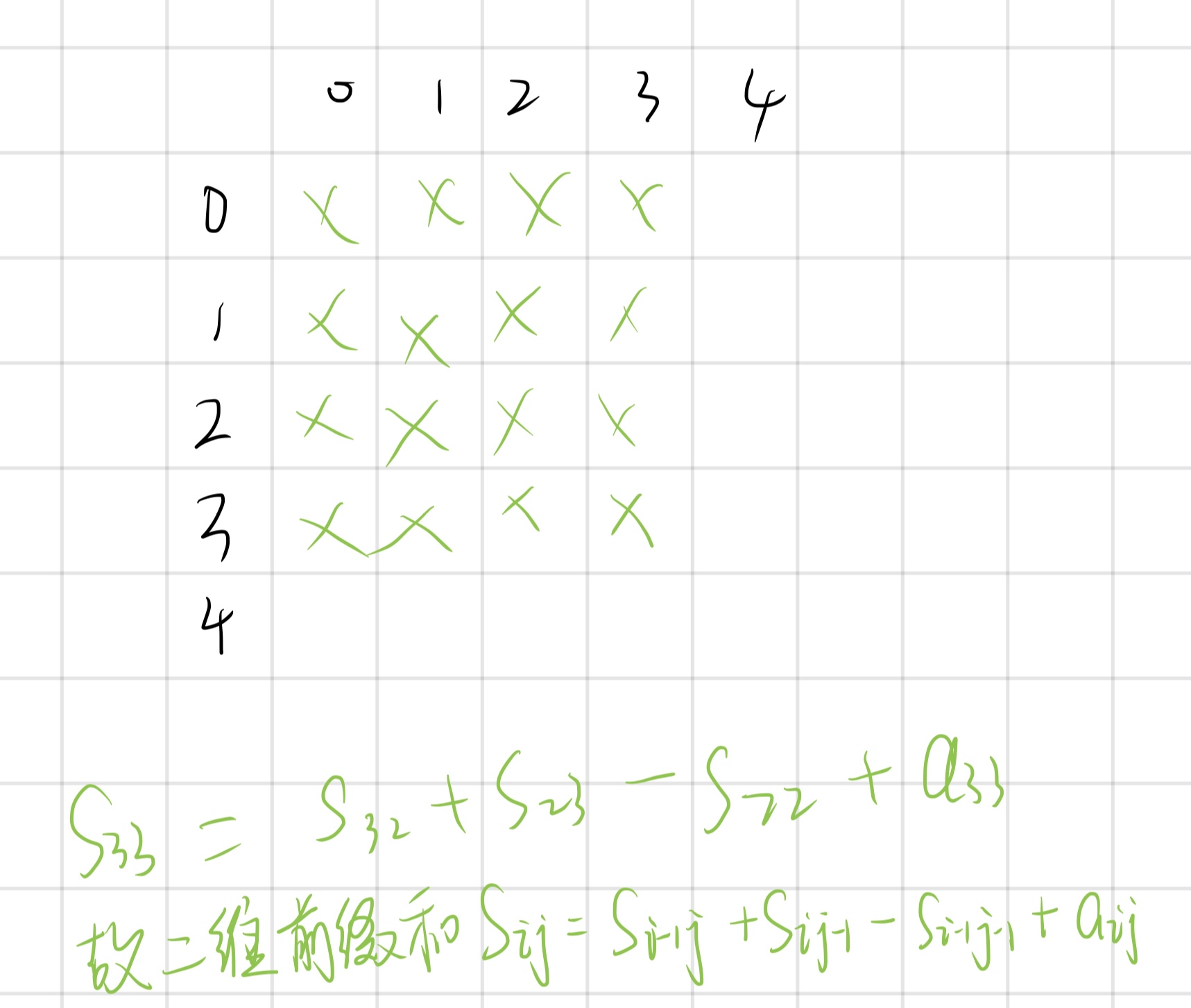什么是前缀和
对于一组数 a1, a2, a3, a4, a5
其前缀和为 Si = a1 + a2 + .. + ai
如何求前缀和
在其中 i 的初始下标为 1, 我们可以得到递推公式 $S_i = S_{(i-1)} + a[i]$
让 i 从 1 开始且定义 S[0] = 0, 这是为了方便我们计算出指定区间的元素和
前缀和有什么用
比如当我们计算区间[l,r]的所有数的和, 就可以直接 S[r] = S[l-1]
现在要求 [1,10]之前的和, 就可以直接 S[10] - S[0]即可得解
即 s[r]-s[l-1]
为啥不直接 for 循环求[l, r]
因为如果我们有很多个 [l,r]区间要求, 那么就得来十次 for 循环, 而采用前缀和只需要一次从头到尾的 for 循环后面直接相减即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
const int N = 100010;
int a[N], S[N];
int main(){
int m,n;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
S[i] = S[i-1] + a[i];
}
for(int i = 0; i < m; i++){
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", S[r]-S[l-1]);
}
return 0;
}
|
例题: 前缀和
二维前缀和
同理, 二维数组的前缀和也是每个 index 对应的 value 之和
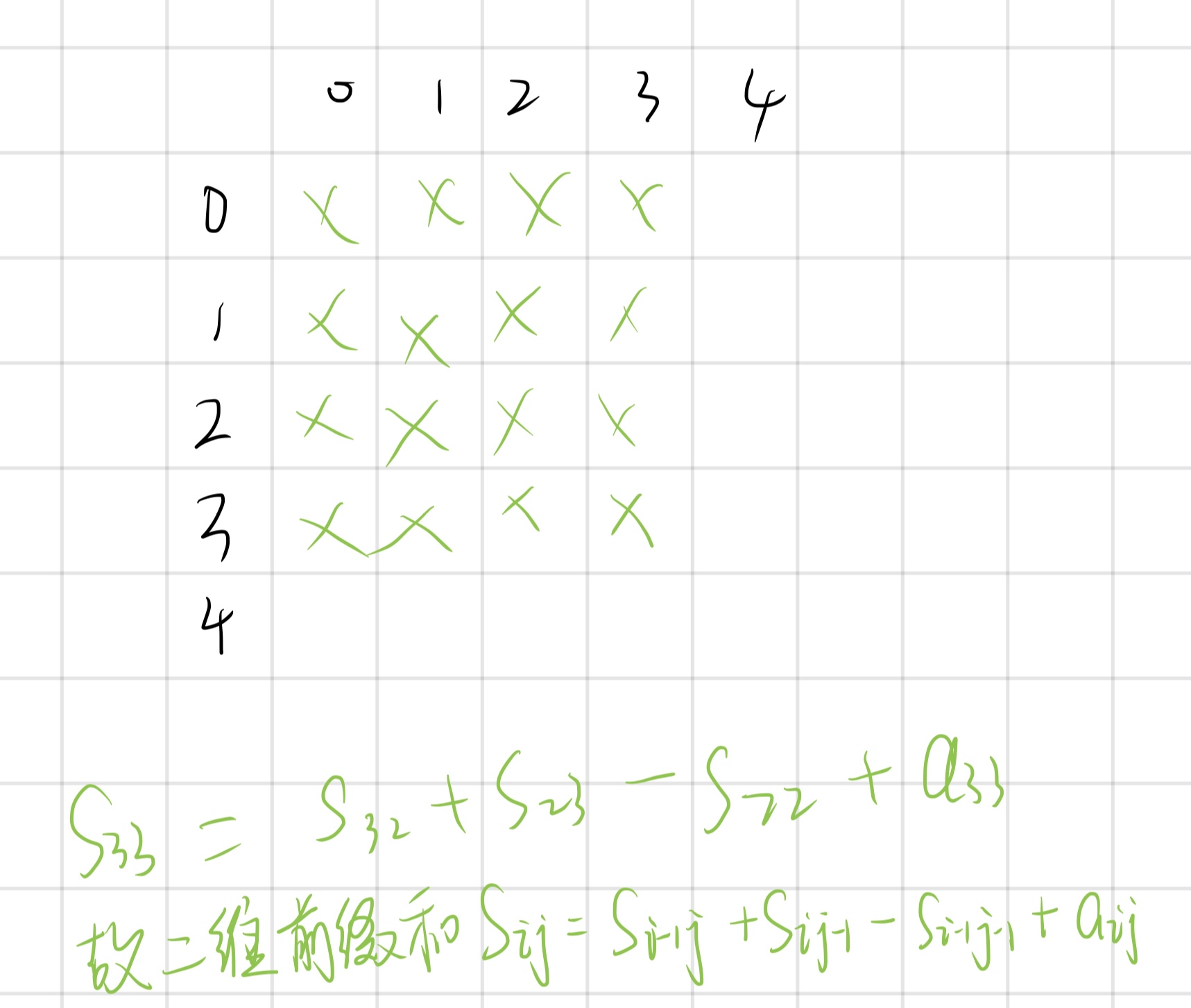
二维前缀和的作用?
求子矩阵的和
现在我们要求 S33 和 S11 围起来的这块子矩阵的和, 那么可以根据前缀和求解.
他等于 S33 - S31 - S13 + a00
可以看到这个一维前缀和s[r]-s[l-1] 是类似的, 只不过最后要加上一块缺的角
即: 求 [x1][y1]到 [x2][y2]的公式为 S[x2][y2] - S[x1-1][y2] - S[x2][y2-1] + a[x1-1][y1-1]
构造二维前缀和
首先肯定要有原始数组矩阵, 这个原始数组最好有效元素都从 index=1 开始
有了原始数组, 就可以从 1 开始构造了前缀和矩阵了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
const int N = 1010, M = 1010;
int a[N][M];
int S[N][M];
int main(){
int n,m,q;
scanf("%d%d%d", &n,&m,&q);
//构造原始数组矩阵
for(int i = 1; i<=n; i++)
for(int j = 1; j <= m; j++) {
scanf("%d",&a[i][j]);
}
//计算前缀和
for(int i = 1; i<=n; i++)
for(int j = 1; j <= m; j++) {
S[i][j] = S[i-1][j] + S[i][j-1] + a[i][j] - S[i-1][j-1];
}
//求子矩阵的和
for(int i=0; i < q; i++){
int x1,y1,x2,y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
int tmp = S[x2][y2] - S[x1 -1][y2] - S[x2][y1-1] + S[x1-1][y1-1];
printf("%d\n", tmp);
}
return 0;
}
|
例题: 子矩阵的和