如何手写一个堆?
堆对外提供哪些 api ?
① 插入一个元素
② 求集合中的最小值
③ 删除最小值
延伸操作:
④ 删除任意一个元素
⑤ 修改任意一个元素
堆的基本结构
堆是一个完全二叉树
完全二叉树: 除了最后一层, 其它层全是非空节点. 最后一层的节点按照从左往右排列, 中间没有空节点
小根堆的性质: 每一个节点都是小于等于左右儿子节点
堆的存储方式
一维数组
完全二叉树都是用一维数组存的
堆的基本操作
一维数组 heap[] 和 数组长度 int size 来完成下面的操作
数组存储所有元素, size 表示有效元素的长度
down 操作
down(x) 将指定元素下沉
当我们修改一个元素后进行 down 操作, 过程如下图
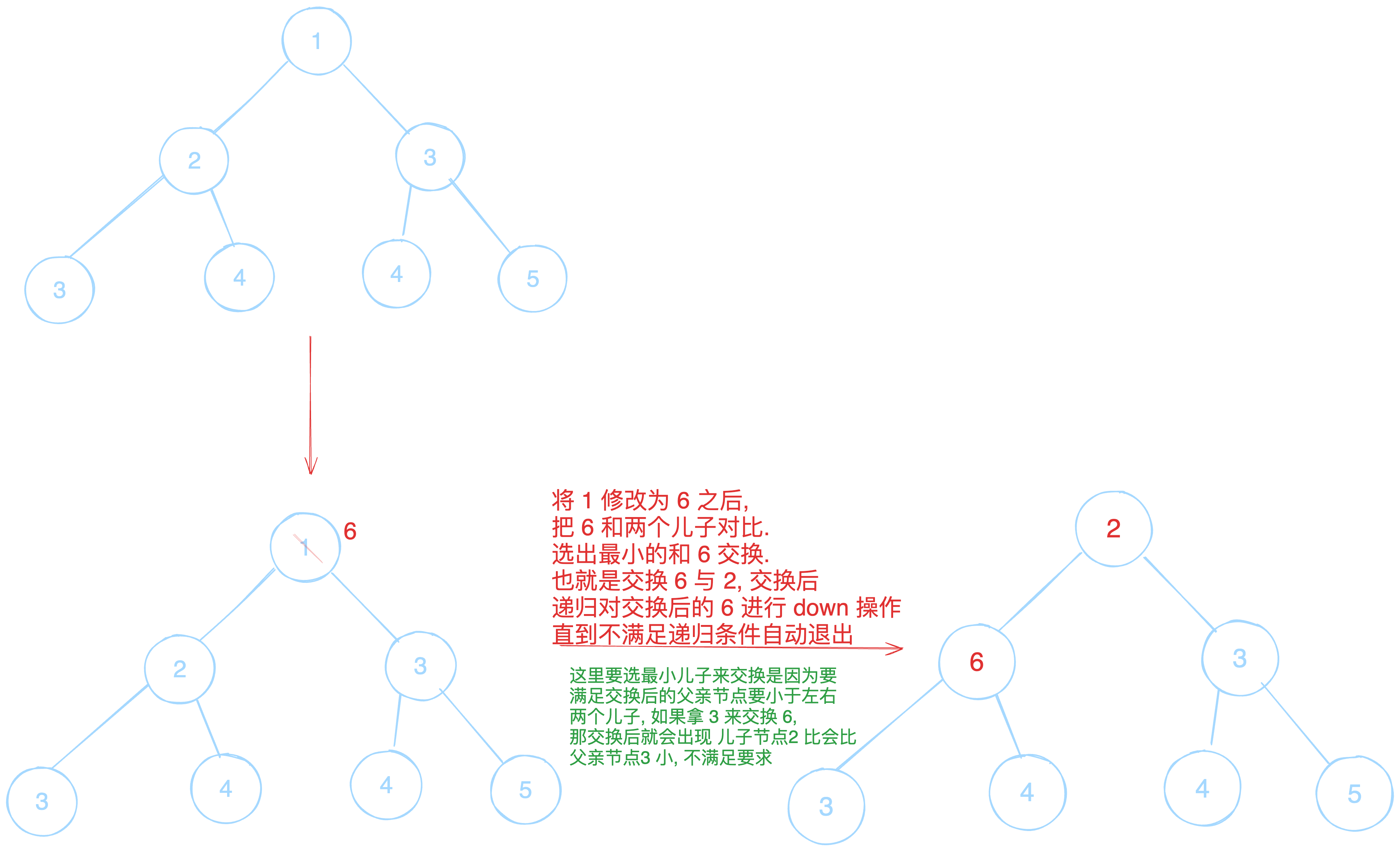
up 操作
up(x) 将指定元素上升
如何从一个一维数组建堆
如果是每次插入一个元素就开始 down, 那么时间复杂度是 NlogN
从 $\frac{n}{2}$ 开始往树根 down 元素, 可以达到 O(N)的时间复杂度
如下图, 对于树中到最后一层节点, 我们是不需要进行 down 操作的, 因为 他们没有儿子节点, down 了也没用, 所以我们从 $\frac{n}{2}$ 开始往树根 down 元素, 也就是圈起来的那一层. 对于这一层, 有 n/4 个元素, 他们需要往下 down 1次, 在往上一层有 $\frac{1}{2} * \frac{n}{4} = \frac{n}{8}$ 个元素, 他们需要往下 down 两次, 以此类推
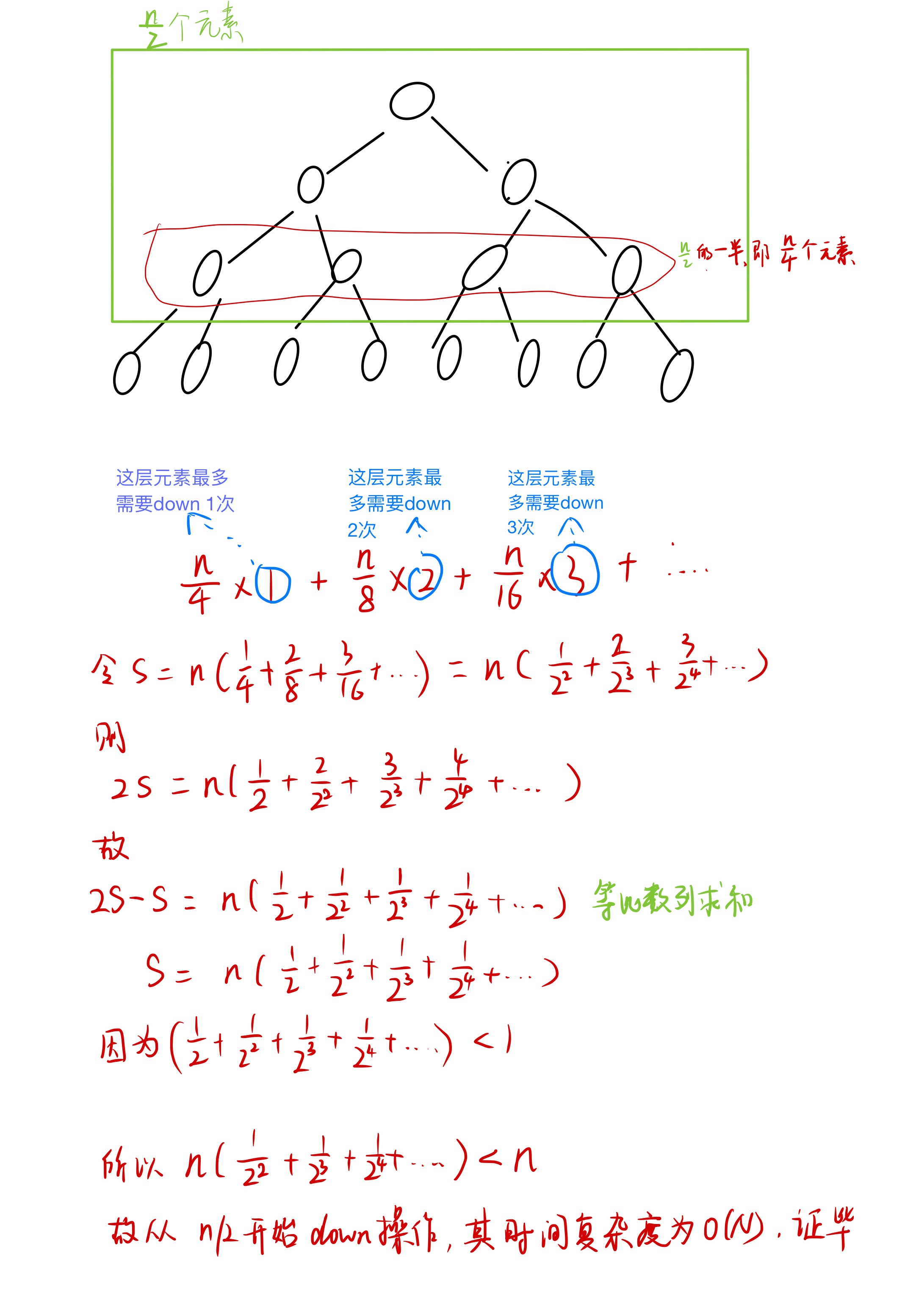
新增元素
直接作为一个新的节点插入到树上. 然后 up 这个节点, 是否能 up 成功, 我们会在 up 操作中判断
修改元素
修改指定元素, 然后无脑执行 up 和 down 操作, 由于 up 操作和 down 操作会自动判断能否 up 或者 down, 所以肯定只有一个操作能成功, 就不需要再修改元素之后考虑应该 up 还是 down 了
删除元素
让最后一个元素覆盖掉指定的元素, 然后 size–. 并且对覆盖后的元素进行 down 操作