并查集优点

并查集是一种数据结构, 对于数据结构, 通常是能够帮助我们快速的执行一些操作才有必要创造出来. 对于并查集, 有如下两个优点

① 快速的判断一个元素是否在集合 A 中

② 快速的把两个集合合并

推导过程

对于判断一个元素是否在集合 A 中可以很容易判断, 常规做法时间复杂度是 O(1), 但是对于把两个集合合并, 就需要遍历其中一个集合, 把遍历到的元素加到另一个集合中, 此时时间复杂度为 O(N).

并查集是利用多叉树来存储数据, 一颗树就是一个集合. 如下图

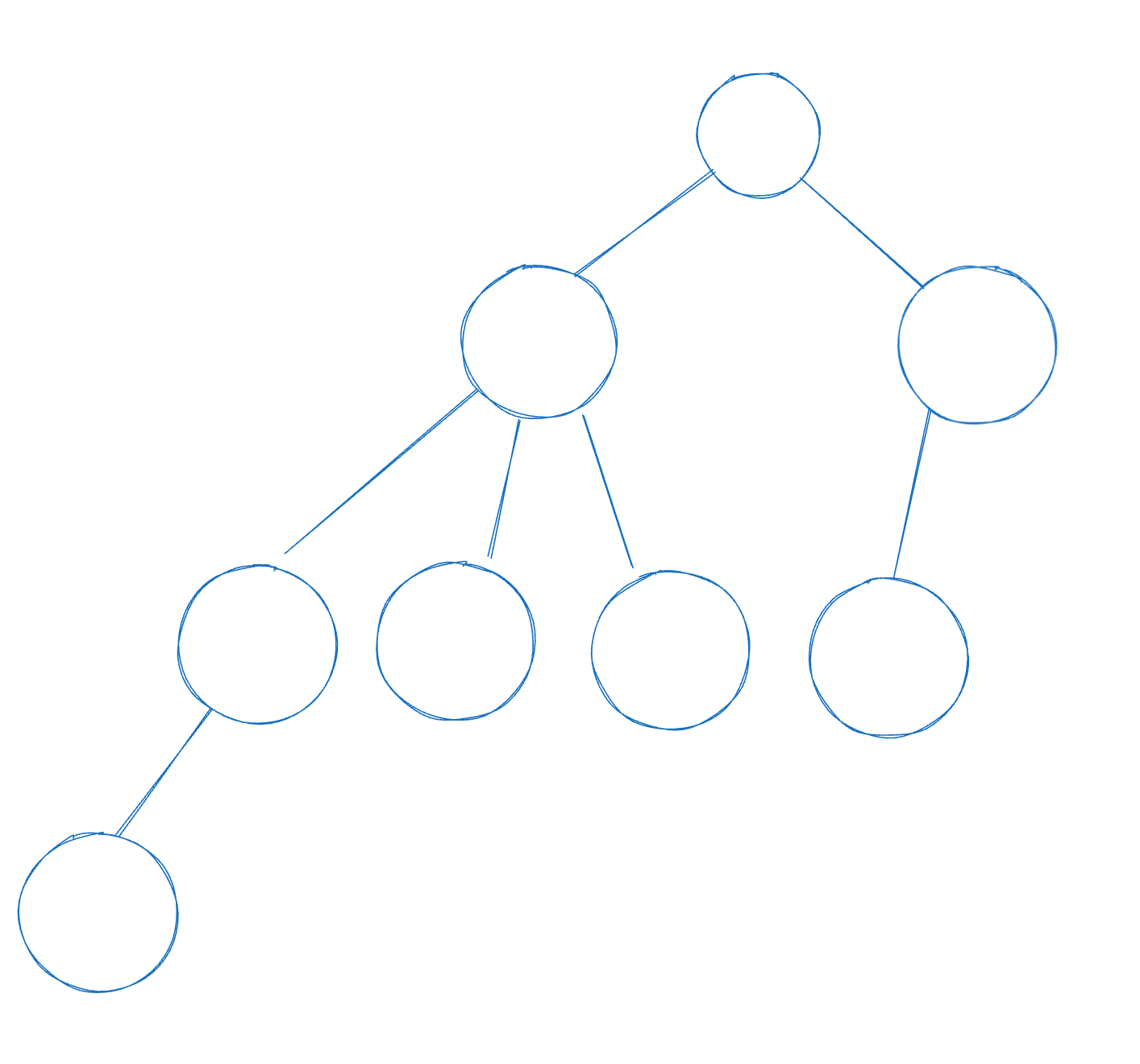
使用数组p[N]建立一个并查集, N表示节点数量或者可能的最大节点数. 对于一个数x, 加入到并查集中, 我们令 p[x] 作为 x 的父节点, 对于根节点, 我们令 p[x] = x

对于一个并查集, 他有如下的操作

① 如何判断树根? — 节点能满足父亲节点是他自身p[x]=x

② 找到一个节点的所在集合的编号(也就是找到祖宗节点) —- 在一个并查集中, 只有祖宗节点能满足父亲节点是他自身p[x]=x, 所以找到祖宗节点可以使用 while 循环直到找到一个满足条件的节点 while(p[x] != x) x = p[x]

③ 合并两个集合 — 把集合 a 的祖宗节点接到祖宗 b 上, 让 a 整个成为 b 的儿子

显然操作①是O(1)的, 操作③在操作②的结果上是 O(1)的.

现在关键就在于操作 ②上, 对于常规的并查集, 我们要找到其祖宗节点, 必然是通过 while 循环来进行寻找, 这就有可能会导致时间复杂度过高. 如下图红色路径

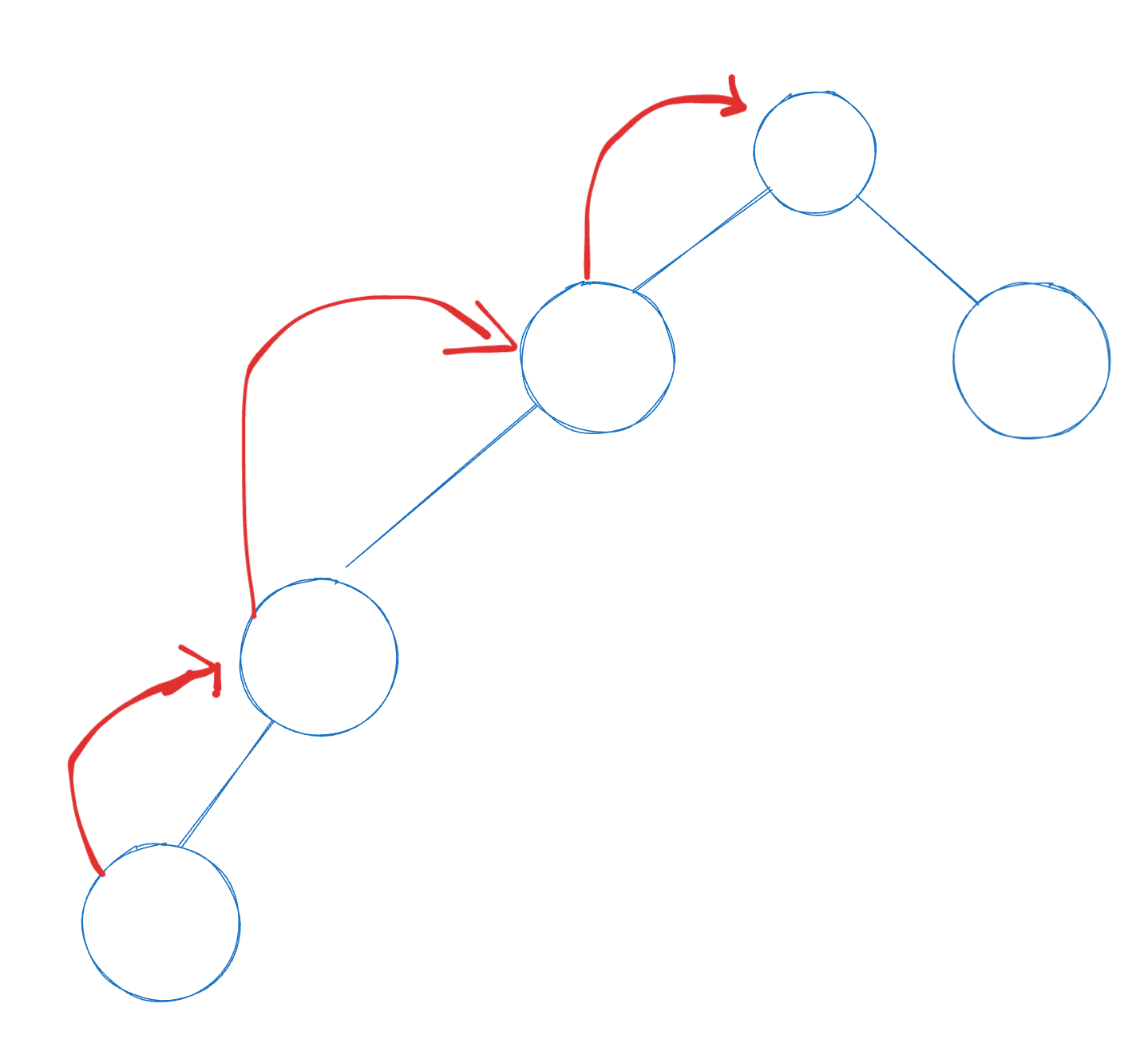
因此, 我们要优化整个过程.

优化方式: 在需要祖宗节点的过程中, 每一个不是祖宗节点的节点, 修改其父节点为祖宗节点, 如下图

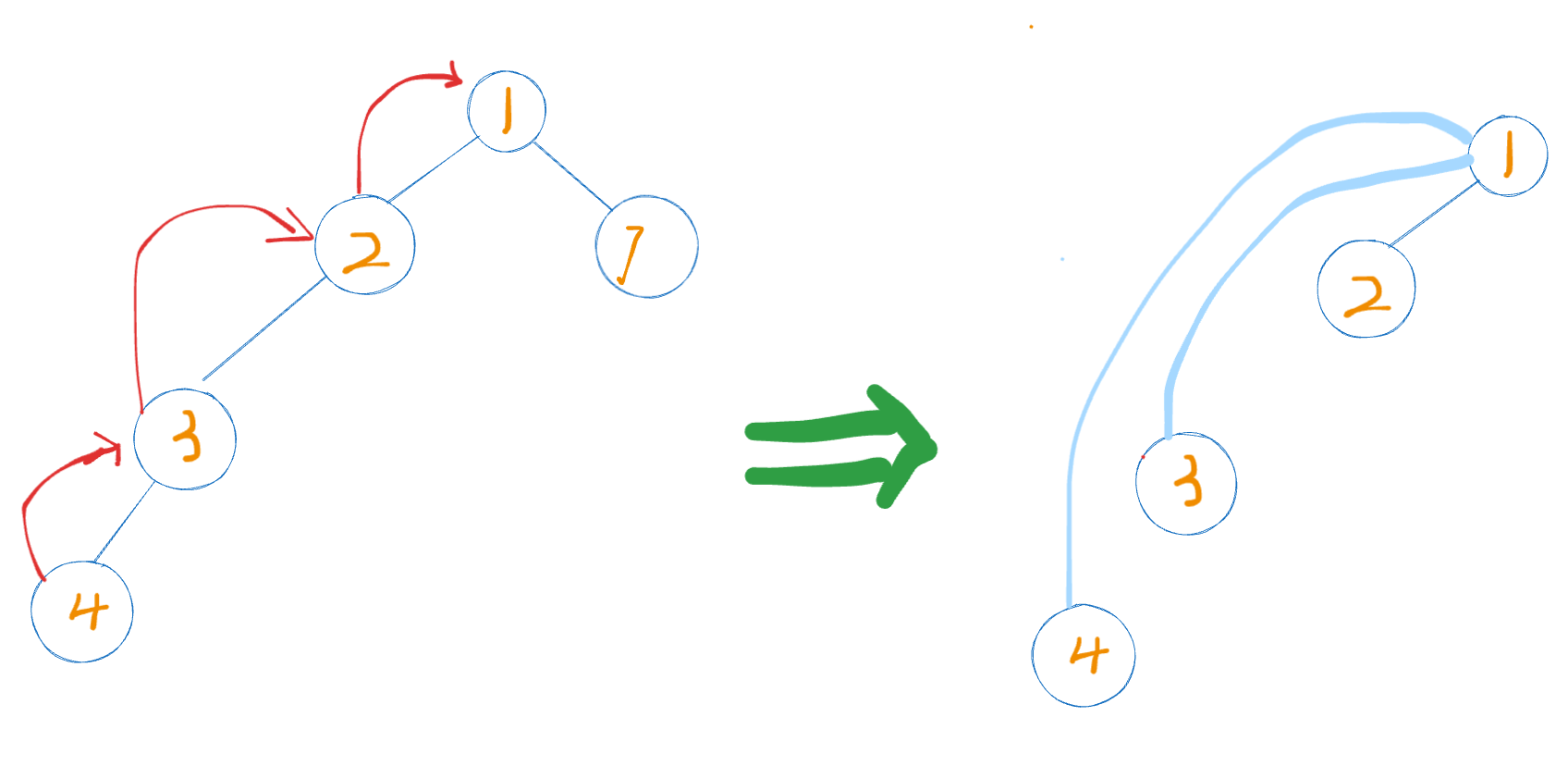
该过程称为 路径压缩

代码

1
2
3
4
5


//返回指定节点的祖宗节点 + 路径压缩
int find(int x){
	if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


#include <iostream>
using namespace std;
const int N = 100010;
int p[N];

//对于任意一个数, 返回其祖先节点. 并在寻找祖先的过程中进行路径压缩
int find(int x) {
    //如果当前节点不是祖先节点, 那么向上寻找祖先节点(等号右边的含义), 找到后, 设置当前节点的父节点为祖先节点(整个等号表达式的含义)
    if(p[x] != x) p[x] = find(p[x]);
    //由于此时父节点就是祖先节点, 故直接返回父节点
    return p[x];
}

int main(){
    int n, m; cin >> n >> m;
    //为每个点建立一个集合
    for(int i = 1; i <= n; i++) {
        p[i] = i;
    }
    while(m--){
        char op[2];
        int a, b;
        scanf("%s%d%d", op,&a, &b);
        //合并操作, 让 a 节点的祖宗节点成为 b 节点祖宗节点的儿子
        if(*op == 'M') p[find(a)] = find(b);
        else printf(find(a) == find(b) ? "Yes\n" : "No\n"); //通过祖宗节点是否相等来判断两个节点是否是同一集合
    }
    return 0;
}

题目:

合并集合

连通块中点的数量

食物链