Trie树的作用: 快速存储和查找字符串集合的数据结构
如何用 trie 树存字符串?
这里提一点, trie 树存储的字符串数量和种类都不会很多, 要么全是小写字母, 要么全是大写字母, 要么全是数字
对于下面的字符串集合
1
2
3
4
5
6
|
abcdef
abcd
aced
bcdf
cdaa
bcdd
|
其 trie 树如下图:
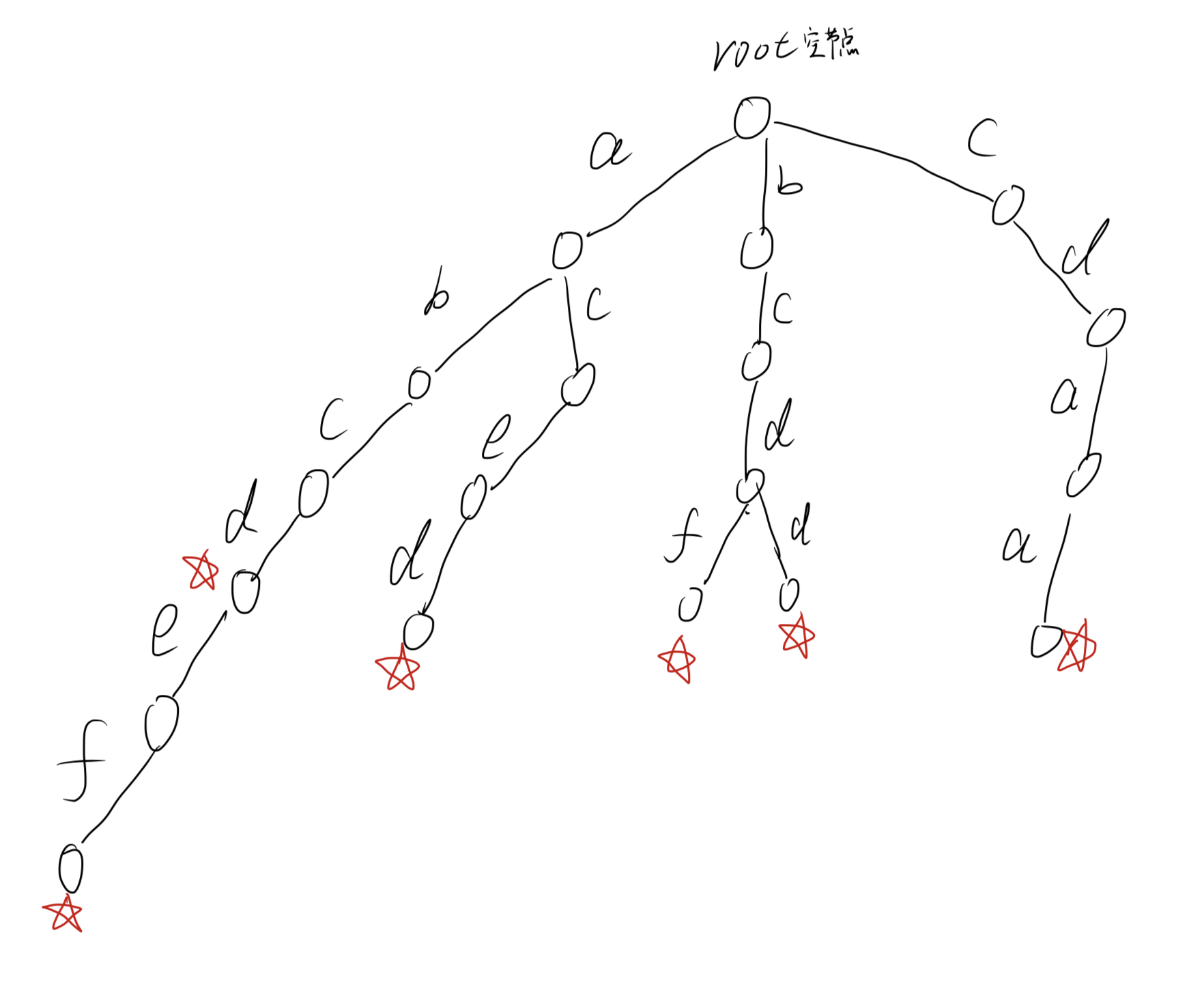
对于一个 trie 树, 我们用一个二维数组$son[m][n]$表示, m 表示节点个数, n 表示一个节点所有可能的儿子数(路径数)
m 一般需要根据题目的输入量级来决定
$n$ 有如下几种可能: ①字母数量, 比如限定全是小写字母, 那么一个节点最多有$n=26$个儿子, 也就是最多 26 条路径 ②数字, 对于一个数字, 用其二进制表示, 那么最多是 $n=2$两种情况
n 往往需要进行从字符到下标的映射或者从数字到下标的映射
从字符到下标: int j = ch - 'a'
从数字到下标: int j = number >> i & 1
在上图中, 使用☆标记了每个字符串的结尾, 所以可以定义一个cnt[] 数组来记录每个字符串出现的次数
图中每个节点是有值的, 但是这个值和字符串无关, 我们定义出一个 idx 指针来指向当前最新的节点, 并在每一次插入时把idx自增, 自增后的坐标值分配给新的节点. 这里 idx 和数组模拟链表中的指针含义类似
模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
const int N = 100010;
int son[N][26], cnt[N], idx;
void insert(char* str)
{
int p = 0;
for(int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p] ++;
}
int query(char* str) {
int p = 0;
for(int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main(){
int n;
scanf("%d", &n);
char op[2], str[N];
while(n --) {
scanf("%s%s", op, str);
if(*op == 'I') insert(str);
else printf("%d\n", query(str));
}
return 0;
}
|
简化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
int son[N][26], cnt[N], idx;
// 0号点既是根节点,又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// 插入一个字符串
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++ idx;
p = son[p][u];
}
cnt[p] ++ ;
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
|
详细注释版:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
#include <iostream>
using namespace std;
//定义最大节点数量
const int N = 100010;
//定义 模拟trie 树的 son 数组; 标记某个字符串出现的次数 cnt[]数组; 指向 trie 树的指针idx, 同时也能表示使用了多少个节点
int son[N][26], cnt[N], idx;
//对于 son[N][26]的下标, 只看一维下标表示某个字符在trie树中的位置, 只看二维下标表示当字符为 N 中的一个时, 他的儿子的下标
//二维下标表示的是字符的映射位置, 所以不管是插入还是查询都需要对一个字符进行下标的映射, 当存储数字时同理
//对于son[i][j]整体: 当字符串 x 映射位置为 i 时, 字符串 y 映射到 j, 此时 son 数组是否有值, 如果有值则说明 y 是 x 的儿子
void insert(char* str) {
//p 指向 root 节点, root 节点不存储数据
int p = 0;
//遍历字符串 str 直到字符为空字符停止遍历
for(int i = 0; str[i]; i++) {
//确定当前字符映射到 son 数组中的位置
int u = str[i] - 'a';
//如果当前指向节点的儿子节点值为 0, 那么说明当前字符需要添加进 trie 树中.
//我们借助 idx 来赋值, 同时让 idx 指向新的节点, 由于 idx=0 时指向root 节点,不存储数据, 所以要先将 idx 自增, 再赋值
//这里是将下一个坐标值赋予新的节点
if(!son[p][u]) son[p][u] = ++idx;
//让 p 指针指向当前节点的子节点
p = son[p][u];
}
//字符串遍历结束, 此时 p 指向字符串最后一个字符所在的节点, 我们对这个节点进行标记, 标记出当前节点是一个字符串的结尾
cnt[p]++;
}
int query(char* str){
int p = 0;
for(int i = 0; str[i]; i++) {
int u = str[i] - 'a';
//查询操作, 没找到子节点, 说明当前字符不在 trie 树中, 那么直接返回0;
if(!son[p][u]) return 0;
p = son[p][u];
}
//p指到了最后一个字符所在的 trie 树节点位置, 由于 cnt 做了字符串结尾标记, 故直接 cnt[p]即可得到字符串在trie树存了几次
return cnt[p];
}
int main(){
int n;
cin >> n;
char op[2], str[N];
while(n--){
scanf("%s%s", op, str);
if(*op == 'I') insert(str);
else printf("%d\n", query(str));
}
return 0;
}
|
题目 最大异或对
这题可以理解数字如何通过二进制表示映射为数组中的二维下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
#include <iostream>
using namespace std;
//一个数有 31 位, 所以 trie 树高为 31 层, 每层最多有 N 个数, 所以节点总数 M 为 31*N
const int N = 100010, M = 31 * N;
//一个节点最多有两个儿子(0 或 1), 所以二维下标长度为2
int son[M][2], idx;
int a[N];
void insert(int x){
int p = 0;
for(int i = 30; ~i; i--) {
int u = x >> i & 1;
//将下一个可分配的坐标值赋予新的节点
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
}
int query(int x){
int p = 0, res = 0;
for(int i = 30; ~i; i--) {
int u = x >> i & 1;
//对第 i 位下标的路径取反, 看看 trie 树上是否存在这个取反的结点
if(son[p][!u]) {
//因为如果存在异或结果为1的数, 那么x和这个数异或之后, 第 i 位一定为 1,
//那么1直接左移i即可得到对应的十进制数, 用res累加即可得到所有能异或为1的位的十进制数之和.
//这样就不需要单独求出异或的数然后再拿x异或了
res += 1 << i;
p = son[p][!u];
}else{
p = son[p][u];
}
}
return res;
}
int main(){
int n ;
cin >> n;
for(int i = 0; i < n; i++) {
scanf("%d", &a[i]);
insert(a[i]);
}
int res = 0;
for(int i = 0; i < n; i++) {
res = max(res, query(a[i]));
}
cout << res;
return 0;
}
|
