单链表
双链表
栈
关于链表, 我们采用数组模拟的方式, 而不是以创建 struct 的方式, 因为new 一个 struct 太慢了, 数据量达到百万级的时候性能低
单链表
用途: 创建邻接表. (邻接表的用途是用来存储树或图)
模拟方式如下:
链表中每个点存两个值: ①自己的 val ②下一个节点的指针
采用两个数组, e数组和 ne数组, e数组用来存储当前节点的值, ne数组用来存储当前节点的下一节点的指针(也就是当前节点的下一个节点在什么位置==> 下一个节点的下标是什么)
e[i]: 位置为 i 的节点的 value
ne[i]: 位置为 i 的节点指向的下一个节点的位置, 还是一个下标
e数组和 ne数组关联的方式是下标来关联
那么对于链表的每个点, 他有两个值, 一个是 e, 一个是 ne, 他们使用下标关联起来的
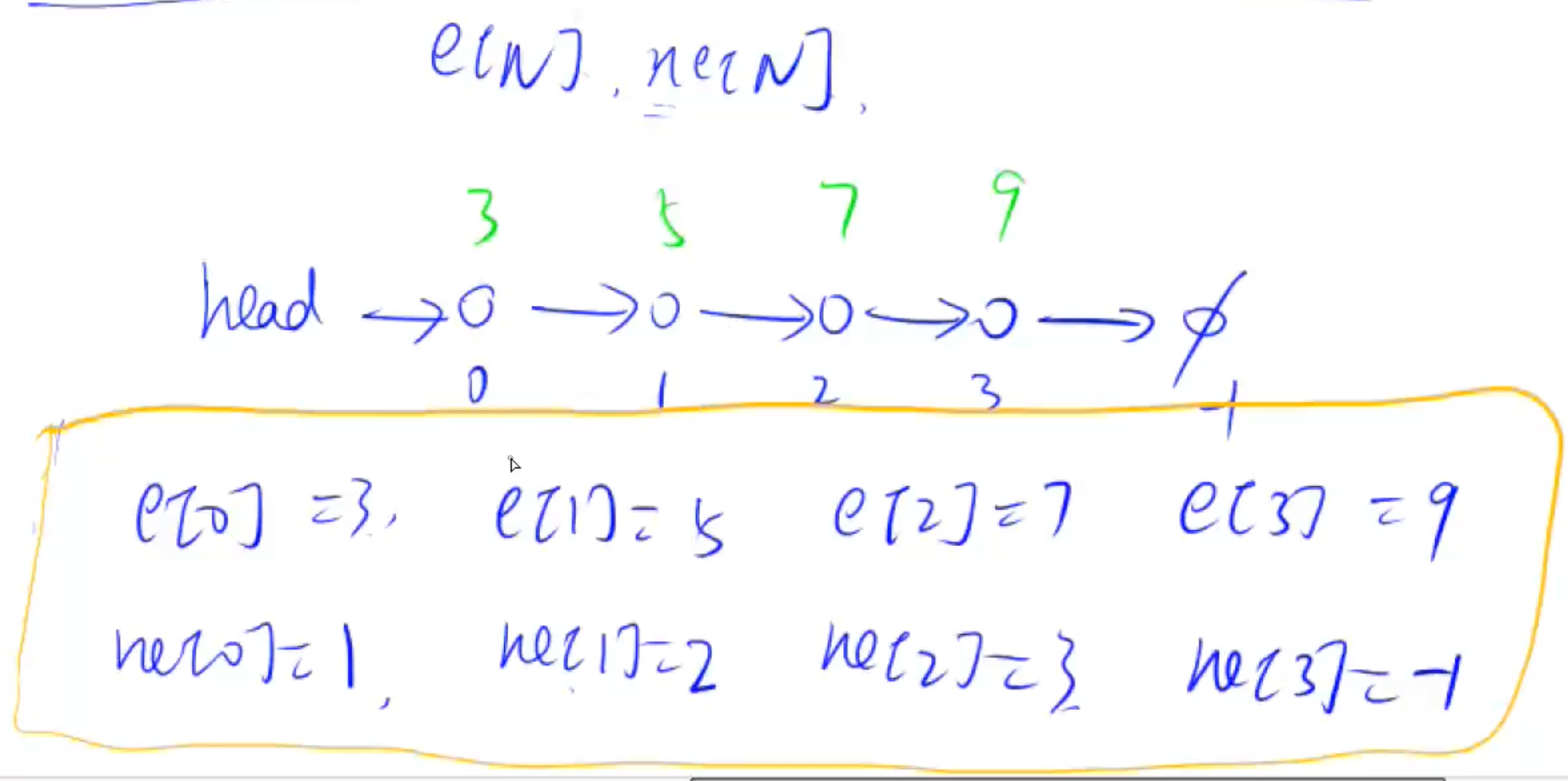
构造一个单链表并给基本的操作方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
const int N = 100010
int e[N], ne[N], head, idx;
void init(){
head = -1;
idx = 0;
}
void addToHead(int x) {
e[idx] = x;
ne[idx] = head;
head = idx;
idx++;
}
void add(int k, int x) {
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
void remove(int k) {
ne[k] = ne[ne[k]];
}
|
注释版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
//构建静态链表的大小----数组模拟链表就是构建了一个静态链表
const int N = 100010;
//head始终表示头结点的下标, idx 表示的是当前操作节点的下标
int e[N], ne[N], head, idx;
//初始化链表
void init(){
//head=-1说明当前为空集
head = -1;
//idx=0表示要操作的节点的下标为 0
idx = 0;
}
//向链表头插入一个数;
void insertHead(int x) {
/*
1. 把这个数存到节点里
2. 让这个节点指向当前的头结点
3. 让 head 指向当前节点
4. idx++, 让他指向下一个要操作的节点
*/
e[idx] = x;
ne[idx] = head;
head = idx;
idx++;
}
// 删除下标为 k 的后一个节点
void remove(int k) {
/*
1. 找到下标为 k 的节点的下一个节点的下一个节点
2. 更新下标为 k 的节点的下一个节点
*/
//ne[k]表示下一个节点的位置, 由于ne[i]表示节点i的下一个节点位置, 所以 ne[ne[k]]表示下标为k的节点的下一个节点的下一个节点
ne[k] = ne[ne[k]];
}
//在下标为k的节点后插入一个节点
void insert(int k, int x) {
/*
1. 把这个数存到节点里
2. 让当前操作节点指向下标 k 的节点的下一个节点
3. 让下标为k 的节点指向当前节点
4. 更新 idx 到下一个要操作的节点, idx++
*/
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
|
题目:
单链表
单链表可能只能建立一个数组模拟链表的初步印象, 在"寻找节点"这一点上, 双链表可以加深理解
双链表
用途: 优化某些问题
单链表的每个节点只有一个指针, 这个指针指向后一个节点
双链表每个节点有两个指针, 一个指针指向前, 另一个指针指向后
对于双链表, 我们直接用数组的 0 位表示 head节点, 1 位表示 tail节点, $l[i]$数组表示下标为 i 的节点的左指针, $r[i]$表示下标为 i 的节点的右指针
初始化
让 head节点右指针指向1(tail节点下标), tail节点左指针指向 0(head 节点下标). 表示空链表. 两个点不表示实质内容, 只表示边界节点
添加节点操作
对于在下标为 k 的节点后面添加节点, 需要① 把新的值存进去 ②让新的节点右指针指向 k 节点的右节点 ③让新节点的左指针指向k 节点的右节点的左节点 ④让 k 节点的右节点的左指针指向当前节点 ⑤让 k 节点的右指针指向当前节点
其中④⑤不能调换顺序, 因为我们只能通过 k 先找到右节点, 然后再把k节点的原右节点的左指针指向当前节点. 如果调换顺序我们就无法通过下标和 r[i]找不到 k 节点的原右节点了
对于在下标为 k 的节点前面添加节点, 那么我们就直接找到下标为 k 的节点的左节点, 然后再调用添加节点到右边的方法就可以了
找到下标为 k 的节点的左节点的方式就是通过 k 来找到, 即 $l[k]$
删除节点操作
也就是让下标为 k 的节点的左节点右指针指向下标为 k 的节点的右节点, 让下标为 k 的节点的右节点的左指针指向下标为 k 的节点的左节点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
const int N = 100010;
int e[N], l[N], r[N], idx;
void init(){
r[0] = 1;
l[1] = 0;
idx = 2;
}
void add(int k, int x){
e[idx] = x;
r[idx] = r[k];
l[idx] = k;
l[r[k]] = idx;
r[k] = idx;
idx++;
}
void remove(int k) {
r[l[k]] = r[k];
l[r[k]] = l[k];
}
|
为什么没有插入头结点的操作?
因为我们没有空指针, 所以直接使用 add 方法来找到对应的位置即可插入头结点
注释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
//声明静态链表长度, 一般由输入的数据量决定
const int N = 100010;
//e[i]表示下标为i的节点的值, l[i]表示下标为i的节点的左指针(左节点下标), r[i]表示下标为i的节点的右指针(右节点下标), idx 表示正在处理的节点的下标
int e[N], l[N], r[N], idx;
//双链表使用两个节点来初始化, 分别是 head 节点和 tail 节点, 互相指向表示空链表, 同时这两个节点可以定义出链表的边界
void init(){
//让 head 节点指向 tail 节点
r[0] = 1;
//让 tail 节点指向 head 节点
l[1] = 0;
//由于 0 1 位置被占用了, 所以 idx 从 2 开始
idx = 2;
}
//add操作表示在 idx 为 k 的节点右边插入节点
void add(int k, int x){
//存储节点值
e[idx] = x;
//让当前操作节点右指针指向下标为k的节点的右节点
r[idx] = r[k];
//让当前操作节点左指针指向下标为k的节点
l[idx] = k;
//让下标为k的节点的右节点的左指针指向当前节点
l[r[k]] = idx;
//让下标为k的节点的右指针指向当前节点 --- 这一步不能和上一步调换
r[k] = idx;
//操作下一个节点
idx++;
}
//注意: 这里的 k 指的值要执行的节点下标而不是说删除第 k 个节点的右一个节点 --- 这是和单链表不同的地方
void remove(int k) {
//让待删除节点的 左节点的右指针 指向 待删除节点的右节点
r[l[k]] = r[k];
//让待删除节点的 右节点的左指针 指向 待删除节点的左节点
l[r[k]] = l[k];
}
|
单链表和双链表的区别
我们都是用数组来模拟链表, 但是这里的模拟方式有区别
① 单链表有空指针, 所以有head 可以为 -1
双链表不表示空指针, 而是直接用固定的两个点0 1 表示 head 节点和 tail 节点, 但是这两个节点不存储任何数据, 仅仅用来限制整个链表的边界
② 初始化方法不同
单链表由于存在空指针, 所以一开始直接让 head 为空指针-1
双链表不存在空指针, 所以用两个端点互相指向来完成初始化
③ 单链表的 head 是表示下标(指针的含义); 双链表的 head, tail 表示的是不存储数值的节点
④ 删除节点操作在单链表中指的是删除 idx 为k 的下一个节点, 在双链表中指的是 idx 为 k 的这个节点本身. 添加节点则和单链表意思一致
题目
双链表
栈
数组模拟栈
1
2
3
4
5
6
7
8
9
10
11
|
const int N = 1000010;
//tt 表示栈顶指针, 这里我们以 0 表示栈中没有元素
int stk[N], tt;
//向栈顶插入元素
stk[ ++ tt ] = x;
//弹出元素
tt--;
//获取栈顶元素
stk[tt];
//判空
if(tt > 0) not empty
|
队列
数组 q[N] , 使用 head 指向队头, tail 指向队尾.
初始化: head=0, tail=-1;
插入: q[++tail] = val
删除: head++
判空: head<=tail 不为空
读取队头元素: q[head]
单调栈
应用场景: 给定一个序列, 求出这个序列中 每一个数 左边最近的比他小的数
1
2
|
序列: 3 4 2 7 5
ans: -1 3 -1 2 2
|
思考过程: 先暴力再优化(类似双指针)
暴力: 要找每一个数左边最近的比他小的数, 那么就可以直接遍历每一个数, 然后对于遍历到的数, 遍历其左边的数
1
2
3
4
5
6
7
8
9
|
for(int i = 0; i< n; i++){
for(int j = i - 1; j >= 0; j--){
if(arr[i] > arr[j]) {
cout << arr[j] << endl;
break;
}
}
cout << "-1" << endl;
}
|
优化: 对于遍历到的数x, 我们把他左边的数放到栈中, 如果当前栈顶元素大于等于x, 那么就说明栈顶元素肯定不是我们需要的, 所以把栈顶元素弹出, 一直找到小于 x 的栈中元素然后停止弹出, 把这个元素输出来, 接下来把 x 加入栈中.
这样做的好处是我们能保证数 x 加入栈之后, 他的左边一定不会有比他大的数, 那么当我们开始遍历 x 右边的数时, 已经被弹出去的栈元素(大于或等于 x)的元素一定不会成为x右边数的答案, 因为 x 是最近的. 这样, 我们就在栈中构成了一个单调增的序列, 也就是单调栈.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
const int N = 100010;
int a[N];
int stk[N], tt = 0;
void pop(){
tt--;
}
void push(int x) {
stk[++ tt] = x;
}
bool empty() {
return !(tt > 0);
}
int query() {
return stk[tt];
}
void find(int n){
for(int i = 0; i < n; i++) {
while(!empty() && query() >= a[i]) {
pop();
}
if(empty()) {
cout << "-1" << " ";
}else {
cout << query() << " ";
}
push(a[i]);
}
}
|
单调队列
应用场景: 滑动窗口中的最大值和最小值
单调队列优化过程: 先考虑暴力怎么做? 然后把其中没有用的元素删掉, 得到单调性, 有单调性的话当我们去求极值, 就可以直接从队列中拿第一个点或最后一个点了
单调队列: 队头出队, 队尾出队入队(注意: 单调队列的队尾是可以出队的)
关于单调栈和单调队列的使用方法
我们先考虑使用栈或者队列时暴力做法是什么? 然后把栈或队列中没有用的元素删除, 观察剩下的元素是否有单调性, 有单调性的话再看看怎么优化这个问题
