1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

typedef <int, int> PII;
void intervalMerge(vector<PII> &input) {
  vector<PII> res;
  int st = -2e9, ed = -2e9;
  sort(input.begin(), input.end());
  for(auto item : input) {
    if(ed < item.first) {
      if(st != -2e9) res.push_back({st, ed});
      st = item.first, ed = item.second;
    }else{
      ed = max(ed, item.second);
    }
  }
  if(st != -2e9) res.push_back(st, ed);
  input = res;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

typedef <int, int> PII;
void intervalMerge(vector<PII> &input) {
  vector<PII> res;
  //维护区间
  int st = -2e9, ed = -2e9;
  //排序, 以左端点从小到大排序, 对于 PII 中, sort 函数会先排序左端点, 再左端点相同时排序右端点
  sort(input.begin(), input.end());
  //开始遍历区间
  for(auto item : input) {
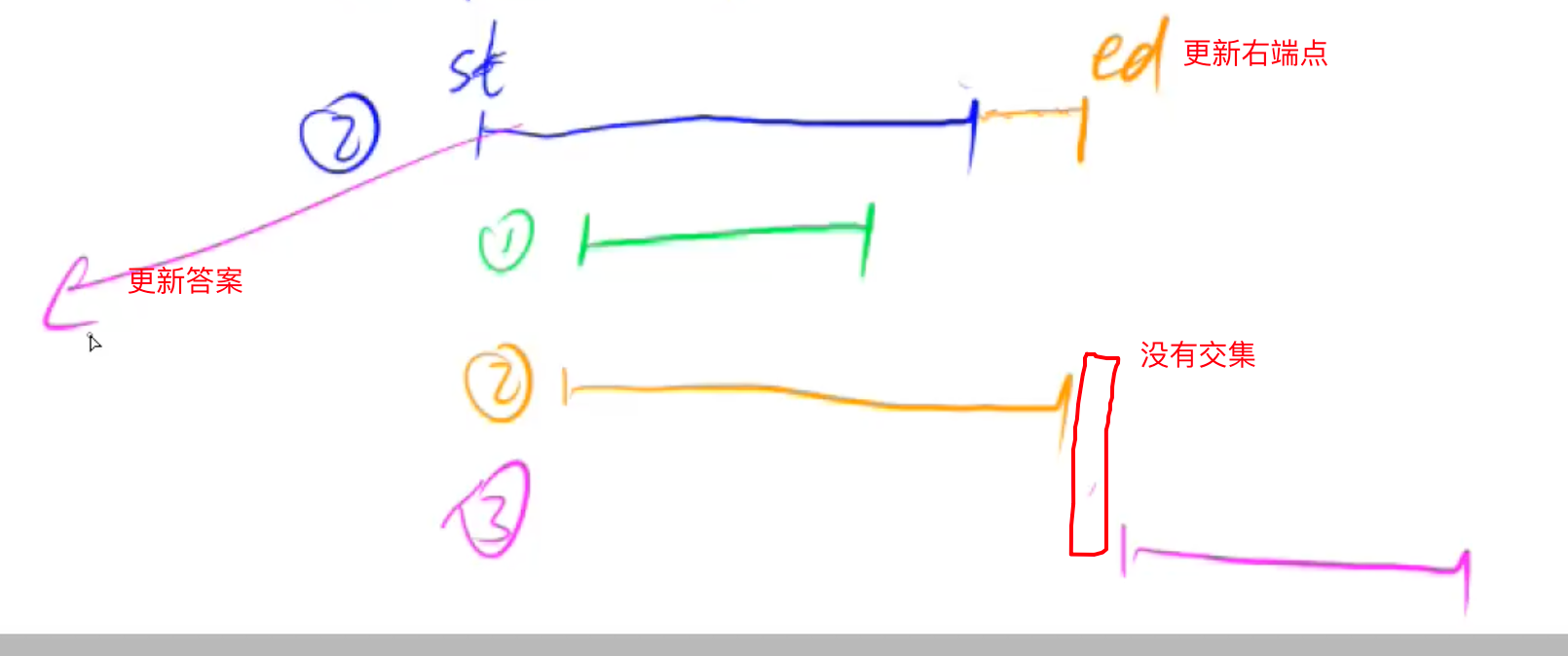
    //如果当前区间的右端点严格小于下一个区间的左端点, 那么说明两者无交集, 此时①添加答案②更新端点
    if(ed < item.first) {
      //注意, 只有维护的区间不是负无穷的区间时, 添加的答案才有意义, 所以要进行一次判断
      if(st != -2e9) res.push_back({st, ed});
      //更新区间为下一个区间
      st = item.first, ed = item.second; 
    }else{
      //区间的右端点大于等于下一个区间的左端点, 对应情况①和情况②, 情况二可直接ed=item.second, 但由于情况一的存在, 所以不能直接ed=item.second, 应该做一个max来校验
      ed = max(ed, item.second);
    }
  }
  //1. 最后一个区间如果和前面的区间是没有交集的, 那么在for循环中会漏掉, 没添加这个区间到结果里, 所以这里要给他加上
  //2. 区间一直在合并, 没有添加区间到答案里, 这里要加上
  //3. 最后两个区间合并了, 没有添加区间到答案里, 这里要加上
  if(st != -2e9) res.push_back(st, ed);
  
  //将 res 赋给 input, 这样调用方就能拿到更新好的结果了
  input = res;
}